Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 3.Problemas - Ex. 29
Dois trens passam pela mesma estação, sem parar nela, com dois minutos de diferença, ambos a . O primeiro a passar viaja rumo ao sul e o segundo para o oeste. (a) Determine o vetor velocidade relativa do seguno trem em relação ao primeiro. (b) Com origem na estação, e tomando como instante inicial o da passagem do primeiro trem pela estação, represente graficamente o vetor deslocamento relativo do segundo trem em relação ao primeiro, nos instantes , e . Que forma tem a trajetória do segundo trem vista do primeiro? (c) A que distância mínima os dois trens passam um do outro? Em que instante isso ocorre?
Passo 1
Vamos começar estabelecendo um par de eixos pra facilitar a nossa solução
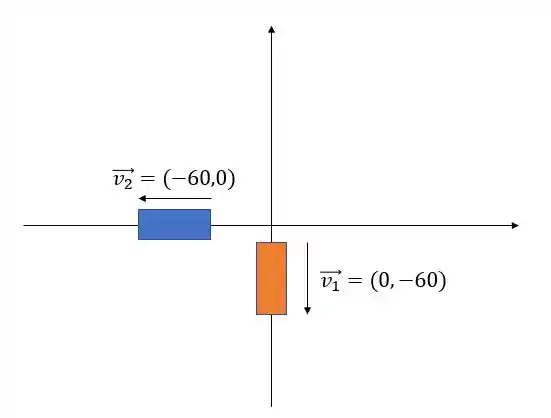
A velocidade relativa entre eles é igual a:
O módulo da velocidade é de:
E aponta na direção noroeste, a ° exatos!
Passo 2
A posição do trem é dada por:
E a posição do trem é dada por:
Então, a posição relativa entre eles é:
Isso é uma reta, que pode ser parametrizada por:
Que é uma reta que aponta na direção noroeste!
Vamos analisar os tempos que ele mandou no enunciado:
: , , .
: , , .
: , , .
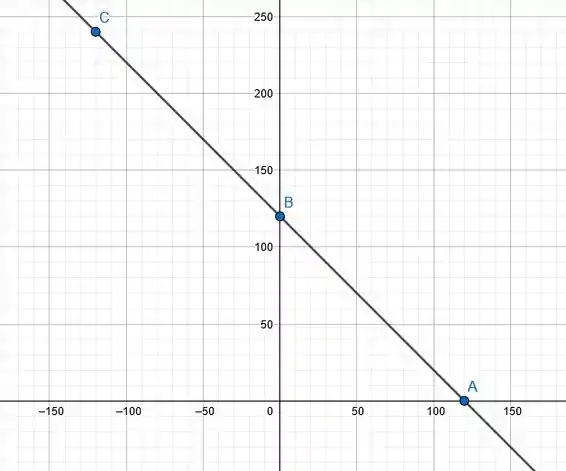
Passo 3
A distância entre os trens é:
O valor mínimo dessa parte com raiz é o mínimo da função do segundo grau:
Que ocorre para min.
Então o valor mínimo de é . Mas isso está numa unidade estranha! Está em . Passando os para :