Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 17.7 - Ex. 66
Dois trens viajam um em direção ao outro a m/s em relação ao solo. Um dos trens faz soar um apito de Hz.
- Que frequência é ouvida no outro trem se o ar está parado?
- Que frequência é ouvida no outro trem se o vento está soprando a m/s no sentido contrário ao do trem que apitou?
- Que frequência é ouvida se o sentido do vento se inverte?
Passo 1
Questão de efeito dopler a gente tem que tomar cuidado quando vai definir o sentido das velocidades. Feito isso, é só colocar na fórmula e ser feliz!
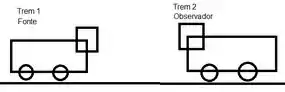
Como o Trem é quem faz soar o apito, ele é a fonte. Assim, o Trem é o observador. Com isso podemos definir os sinais das velocidades, já que o valor já foi dado no enunciado. O sentido positivo é definido como sendo OBSERVADOR FONTE, sendo assim todas as velocidades que forem da direita para esquerda serão positivas.
Definindo isso, temos agora as velocidades da fonte e do observador e a frequência da fonte:
FONTE: ; .
OBSERVADOR: .
Obs: antes de passar para o passo, é importante olhar as unidades! Se elas estiverem ok, segue o baile!
Passo 2
Na letra é pedido a frequência que é ouvida no outro trem se o ar está parado.
Aí você me pergunta: onde entra o vento nisso tudo?
Lembra que eu falei que depois de definir o sentido era só aplicar na fórmula? Pois bem, na relação geral do efeito dopler entra a velocidade de propagação da onda no meio. Na maioria dos casos, esse meio é o ar e a velocidade de propagação é m/s. No entanto, se tiver vento (vamos ver mais a diante), temos que modificar um pouco essa velocidade.
Queremos então a frequência ouvida no outro trem, no nosso caso é o Trem , no observador . A fórmula do efeito dopler nos diz que:
Onde é a velocidade de propagação do som no meio, é a velocidade da fonte e é a velocidade do observador. Como o vento está parado é apenas a velocidade do som m/s e como já definimos os sinais de e , é só colocar na fórmula:
Passo 3
Barbada né?! Agora vamos para a letra .
Agora o problema pede para calcular a frequência no outro trem de novo (Trem – observador ), mas agora com o adicional do vento que se propaga ‘no sentido contrário ao trem que apitou’. Se o trem que apitou é o Trem, então o sentido contrário é o mesmo sentido do Trem. Logo, o vento se propaga no sentido positivo, da direita para a esquerda. Lembrando que a nova velocidade do som, quando tem vento é dada por:
- (quando a velocidade do vento for na mesma direção de propagação do som);
- (quando a velocidade do vento for contrária a velocidade de propagação do som);
- Quando não há vento, como no caso da letra (a), .
Nosso caso é o segundo, logo a velocidade do som vai ser
Organizando os dados, temos:
FONTE: ; .
OBSERVADOR: .
VEL. SOM: .
Agora é só colocar na fórmula!
Passo 4
Tudo bem até aqui? Bora pra letra ()!
Agora o enunciado pede que frequência é ouvida (ou seja, no mesmo observador, Trem), mas agora com a velocidade do vento invertida. Então a única mudança aqui é :
Organizando os dados, temos:
FONTE: ; .
OBSERVADOR: .
VEL. SOM: .
Agora é só substituir na fórmula!
Pronto! ;)