Uma menina está sentada perto da janela aberta de um trem que viaja para leste com uma velocidade de 10 m/s. O tio da menina está parado na plataforma e observa o trem se afastar. O apito da locomotiva produz um som com uma frequência de 500 Hz. O ar está parado.
- Que frequência o tio ouve?
- Que frequência a menina ouve?
- Que frequência o tio passa a ouvir?
- Que frequência a menina passa a ouvir?
Um vento vindo do leste começa a soprar a 10 m/s,
Passo 1
Olá galera, tudo bem? Bora resolver essa questão?
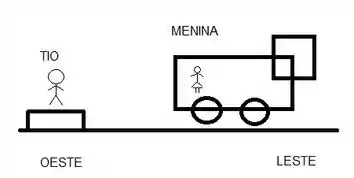 Primeiro precisamos montar um desenho para entender melhor o que está acontecendo!
Primeiro precisamos montar um desenho para entender melhor o que está acontecendo!
Vamos agora definir quem é a fonte e quem é o observador, pois assim saberemos os sinais das velocidades de cada um.
Como o apito sai do trem, ele vai ser a nossa fonte. Assim, o tio na plataforma representa o observador. O sentido positivo (também a velocidade do som) é TIO MENINA (ou seja oeste para leste), pois vai sempre do observador para a fonte. Pelo enunciado, sabemos que o trem está indo para o leste, então a velocidade da fonte é positiva. Já o tio está parado na plataforma, logo a velocidade dele (do observador) é zero.
O enunciado também diz que o ar está parado. Isso significa que a velocidade de propagação da onda no meio é a velocidade do som .
Tudo bem até aqui? Ok! Agora vamos ao que se pede!
Passo 2
Na letra () é solicitado a frequência que o tio ouve. Para isso, temos os seguintes dados:
FONTE (trem/menina): ; (velocidade da fonte= Oeste/Leste , sentido positivo)
OBSERVADOR (tio): (observador em repouso) ;
.
Agora é só usar a fórmula geral do efeito dopler!
Ok? Vamos para a letra ()?
Passo 3
A letra () pergunta o que a menina ouve.
A fonte continua sendo o trem, mas agora quem é o observador é a menina. A velocidade do observador tem mesmo módulo e direção que a velocidade do trem.
Lembrando que o sentido positivo é OBSERVADORFONTE, ou seja, OESTELESTE.
Sendo assim, temos:
FONTE: trem
(Oeste/Leste)
OBSERVADOR: menina
(Oeste/Leste)
Som: como não há vento (AINDA! MUAHAHA), a velocidade de propagação no meio é a própria velocidade do som
Olha só na fórmula como fica:
A frequência que a menina ouve é a mesma emitida pela fonte! E faz sentido! O efeito dopler é um efeito que aparece quando temos um movimento relativo de fonte e observador. Nesse caso, a velocidade relativa entre eles é nula, então o efeito dopler é zero e a frequência ouvida não sofre alteração.
E que tal adicionarmos agora um ventinho? Vamos pras letras e!
Passo 4
Na letra () o problema adiciona um vento vindo do LESTE, e pergunta que frequência o TIO passa a ouvir. Agora voltamos à mesma situação da letra (), no qual a FONTE = TREM/MENINA e OBSERVADOR = TIO. E o sentido positivo é TIO-MENINA (Oeste-Leste)
Se o vento vem do leste, quer dizer que ele vai para oeste, certo? E o som, para sair do trem e chegar no tio da menina, ele tem que se propagar do leste para o oeste também, certo? Ou seja, o vento está a favor da direção de propagação, ambos viajam do leste para o oeste!
Ta, mas no que isso influencia? Na velocidade de propagação, minha gente!
Se o vento estiver a favor da velocidade de propagação, nós somamos as duas velocidades ( ). Mas, se o vento estiver contra, então subtraímos ( ).
Assim, as velocidades e frequências nessa situação é:
FONTE (trem/menina): ;
OBSERVADOR (tio): (observador em repouso) ;
.
Agora é só colocar na fórmula!
Vamos pra última letra?
Bora lá!
Passo 5
Na letra () é perguntado, com o adicional do vento, o que a menina ouve?
Bom, sabemos da letra (b), que a menina se torna o observador e o trem segue sendo a fonte. E que a velocidade relativa entre eles é nula.
A única coisa que modifica é a velocidade de propagação do som no meio, que é alterada pelo vento. Considerando que a menina está atrás do apito, a ideia aqui é a mesma da letra anterior! O som, para chegar na menina, precisa viajar do leste para o oeste. Como o vento tem essa mesma direção Leste-Oeste, a velocidade do som vai ser .
A velocidade da menina (observador) ainda é m/s, na direção Oeste-Leste, a mesma do trem.
Juntando os dados temos:
FONTE (trem): ;
OBSERVADOR (menina): ;
.
Agora é só colocar na fórmula!
Encontramos novamente o valor de ! E faz sentido? Sim! Pois, mesmo que haja vento, as velocidades tanto da fonte, quanto do observador não foram alteradas, e o observador continua recebendo a mesma frequência emitida da fonte. Lembra, o efeito dopler surge na decorrência de um afastamento/aproximação da fonte em relação ao observador. Se não temos nem afastamento nem aproximação, a frequência não é alterada! Divertido né? =D
Até a próxima pessoal!