Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 18.4 - Ex. 34
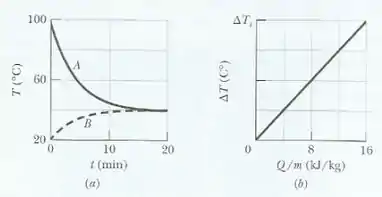
Duas amostras, A e B, estão a diferentes temperaturas quando são colocados em contato em um recipiente termicamente isolado até entrarem em equilíbrio térmico. A figura 18-34a mostra as temperaturas das duas amostras em função do tempo . A amostra A tem uma massa de ; a amostra B tem uma massa de . A figura 18-34b é um gráfico do material da amostra que mostra a variação de temperatura que o material sofre quando recebe uma energia na forma de calor; a variação está plotada em função da energia por unidade de massa do material definida por . Qual é o calor específico do material da amostra A?
Passo 1
Show de bolinhas galerinha, esse exercício envolve misturas em um recipiente isolado termicamente, sendo assim sabendo que todo calor cedido por uma amostra será absorvido pela outra até que o equilíbrio térmico seja atingido. A temperatura final será igual para ambas as misturas. Dessa forma:
Mas para isso, precisamos determinar cada um dos calores separadamente.
Passo 2
Como a temperatura está variando, o calor da amostra A é denominado calor sensível, tal que:
Logo:
Pelo gráfico (a) podemos perceber que a amostra B tem uma variação de temperatura de , e a malandragem é a gente perceber que a inclinação da reta é igual ao calor especifico do material , , tal que:
Como essa amostra tem , então:
Tal que:
Passo 3
Iradoso, agora que conseguimos o valor do calor de cada amostra podemos substituir na equação:
Tal que:
Portanto:
