Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 22.6 - Ex. 31
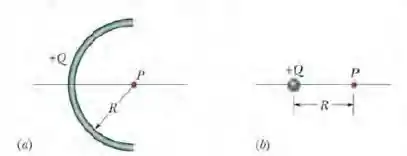
Fig. 22-50a mostra uma barra não condutora com uma carga distribuída uniformemente. A barra forma uma semicircunferência de raio e produz um campo elétrico de módulo no centro de curvatura . Se a barra é substituída por uma carga pontual situada a uma distância do ponto (figura 22-50b) qual é a razão entre o novo valor de e o antigo valor?
Passo 1
E aí, pessoal! 😁
Nesse problema temos uma barra não condutora com uma carga distribuída uniformemente. A barra forma uma semicircunferência de raio e produz um campo elétrico de módulo no centro de curvatura .
Se a barra é substituída por uma carga pontual situada a uma distância do ponto queremos saber qual é a razão entre o novo valor de e o antigo valor.
Parece complicado? 👀
Para resolver esse problema basicamente temos que obter a equação do campo elétrico para o arco e para a carga pontual e obter a razão entre elas.
Bora lá! 😉
Passo 2
Primeiramente, vamos calcular o campo devido ao arco, que tem densidade linear , em que é o comprimento de arco. Para essa questão, temos que saber o campo elétrico produzido por um arco de circunferência carregado (se quiser a dedução, está presente num exemplo no início do capítulo):
Como nesse caso, , e , temos:
Tranquilo até aqui? 😬
Passo 3
Agora, como sabemos, o módulo do campo produzido por uma carga pontual é:
Então, a razão é:
Para , que é o caso da questão:
E aí! entendeu tudo? Responde Aí! 😁
