Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 22.6 - Ex. 32
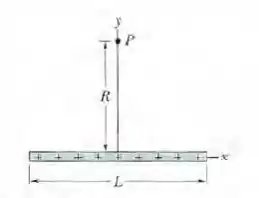
Na Fig. 22-51, uma carga positiva está distribuída uniformemente em uma barra fina, não condutora, de comprimento . Determine (a) o módulo e (b) a orientação (em relação ao semieixo x positivo) do campo elétrico produzido no ponto , situado na mediatriz da barra, a uma distância da barra.
Passo 1
E aí, pessoal! 😎
Nesse problema temos uma carga positiva está distribuída uniformemente em uma barra fina, não condutora, de comprimento e nosso objetivo é determinar o módulo e a orientação (em relação ao semieixo x positivo) do campo elétrico produzido no ponto , situado na mediatriz da barra, a uma distância da barra.
Parece complicado? 🤔
Bem, vamos considerar um elemento infinitesimal da barra , então uma carga infinitesimal da barra é , em que é a densidade linear de cargas.
Por simetria, vemos que as componentes horizontais do campo elétrico de cada elemento infinitesimal se anulam. Portanto, precisamos apenas somar as componentes verticais na integração. Por simetria da barra, basta a gente calcular o campo elétrico em metade da barra ( e multiplicar o resultado por 2. A imagem do campo agindo no ponto P seria mais ou menos essa:
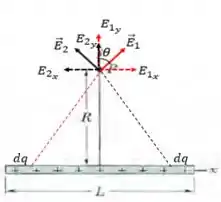
Só que as componentes horizontais de cada campo se cancelam, pois são iguais, apenas com sentidos opostos. E as componentes verticais se somam, mas, como são iguais em módulo, a resultante é o dobro de uma delas.
Para pegar a componente vertical, devemos multiplicar por em que é o ângulo entre o vetor campo elétrico e o eixo y, ou seja, queremos . Nesse caso, vemos que . Essa fórmula vem desse triângulo aqui:
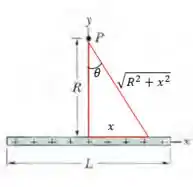
Veja só! 😁
Passo 2
Item (a)
Para calcular o campo elétrico, temos que considerar um campo elétrico devido a um pedaço infinitesimal da barra, dessa forma, como queremos a componente
Agora devemos integrar em toda a barra, colocando os limites de integração na metade da barra, mas multiplicando toda a integral por 2:
Substituindo (como vimos no primeiro passo), e (que é a distância de um ponto na barra para o ponto P). Além disso, podemos jogar o para fora da integral, pois é um termo constante:
Vamos tirar e da integral, por serem constantes, e arrumar um pouquinho a expressão:
Onde .
Cara, essa integral não é tão simples. Para resolver ela, teria que fazer a substituição trigonométrica e fazer as contas. Só que é bem difícil de cobrarem essa resolução em prova, normalmente a resposta dessa integral é dada no formulário. Então, para não ficar uma resolução muito grande, confia em mim! No fim do dia, teremos esse cara:
Substituindo os limites de integração:
Tranquilo até aqui? 😉
Passo 3
Podemos simplificar :
Arrumando essa fração:
Fazendo o mmc dentro da raiz:
Tirando o que apareceu na raiz:
Arrumando de novo:
Substituindo os valores, passando e para metros:
Podemos simplificar o :
Fazendo as contas:
Bacana, não é? 😬
Passo 4
Item (b)
Como falamos no item (a), o campo é vertical no sentido do semieixo y positivo, isto é, faz um ângulo de 90° com o semieixo positivo.
E aí! entendeu tudo? Responde Aí! 😬
Resposta
90° com o semieixo x positivo.