Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 22.6 - Ex. 30
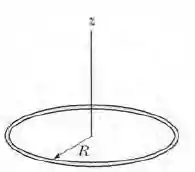
Uma barra fina não condutora, com uma distribuição uniforme de carga positiva , tem a forma de uma circunferência de raio fig. 22-49. O eixo central do anel é o eixo , com a origem no centro do anel. Determine o módulo do campo elétrico (a) no ponto e (b) no ponto . (c) Em termos de , para que valor positivo de o módulo do campo é máximo? (d) Se e , qual é o valor máximo do campo?
Passo 1
E aí! tudo certinho? 😉
Nesse problema temos uma barra fina não condutora, com uma distribuição uniforme de carga positiva , tem a forma de uma circunferência de raio .
A partir daí queremos saber qual é o módulo do campo elétrico no ponto e no ponto sendo o eixo que passa no centro da circunferência. Além disso, em termos de , para que valor positivo de o módulo do campo é máximo? E se e , qual é o valor máximo do campo?
Parece complicado, não é? 😐
Para essa questão, temos que saber a fórmula de cálculo do campo elétrico de um disco de raio a uma distância dele. Você lembra? Essa fórmula está aqui embaixo:
Em que:
- é a densidade superficial de cargas (;
- é a distância no eixo do disco;
- é o raio do disco.
Veja a imagem abaixo:
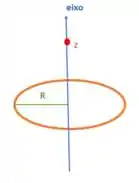
Legal, né? 😬
Passo 2
Bom, mas no centro do disco (), o campo será nulo. Isso se explica por simetria, pois teremos um vetor na extrema direita do anel se cancelando com a extrema esquerda. Só que isso se repete em todo o anel.
Portanto, para cada vetor de um lado do anel, teremos outro do lado oposto que se cancelará com o primeiro. Tipo assim:
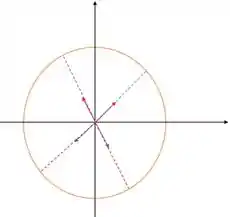
Só que acontecendo em todo o anel. Beleza?? Com isso, o vetor resultante será nulo!
Tranquilo até aqui? 😉
Passo 3
Item (b) no ponto , o campo será:
Ou seja, o termo:
Logo, o campo será igual a zero:
Portanto
O que faz muito sentido, não? Pensa comigo que o campo elétrico vai enfraquecendo conforme nos distanciamos da carga que o gera, até um momento que ele é igual a zero!
Passo 4
Para responder o item (c), pegaremos a equação do campo elétrico devido a um anel em função da distância até o mesmo:
Substituindo , chegaremos em:
Nós vamos descobrir ondo o campo é máximo se derivarmos o campo e igualarmos a zero.
Isso significa derivar essa equação em relação a e igualar a zero (para achar o que deixa o campo elétrico máximo):
Obs: Lembra de máximos e mínimos lá de cálculo? 👀
Vamos colocar tudo que não depende de para fora da derivada:
Pela regra da derivada da divisão:
Vamos multiplicar passar para o outro lado:
Agora podemos nos livrar desse denominador que passa para o outro lado multiplicando:
Isolando de um lado só:
Chegamos a:
Esse é o valor de para o qual o campo elétrico é máximo!
Passo 5
Item (d)
Utilizando novamente a equação do campo elétrico devido a um anel:
Os dados do enunciado são:
- R = 2,00 cm e Q = 4,00 μC
Lembrando que para o campo elétrico máximo e a constante :
E finalmente...
E aí! o que achou? Responde Aí! 😬
