Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 22.Problemas desafioadores - Ex. 67

Uma região do espaço contém uma carga positiva Q que está distribuída uniformemente ao longo de uma esfera de tal modo que a densidade volumétrica de carga ρ r é dada por:

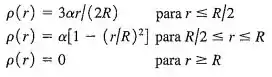
Nessas relações, α é uma constante positiva com unidades de C / m 3 . a Determine α   em função de Q e de R . b Aplicando a lei de Gauss, deduza uma expressão para o módulo do campo elétrico em função da distância r . Faça esse cálculo separadamente para cada uma das três regiões. Expresse suas respostas em termos da carga total Q . c Que fração da carga total está contida no interior da região R / 2 ≤ r ≤ R ? d Qual é o módulo do campo elétrico E → para r = R / 2 ? e Se um elétron com carga q ' = - e for liberado a partir do repouso, em qualquer ponto de qualquer uma das três regiões, o movimento resultante será oscilatório, porém não será harmônico simples. Por quê? (Veja o problema desafiador 22.66 .)

Passo 1

Para iniciarmos esse exercício, precisamos lembrar que a carga elétrica pode ser definida em função da densidade volumétrica de carga e do volume da superfície em questão, ou seja:

Q = ∫ ρ d V

Assim, a carga total na esfera é dada pela soma da carga em cada uma das regiões e é possível isolar α no resultado obtido.

Logo, para r ≤ R / 2 :

Q 1 = ∫ 0 R / 2 3 α r 2 R 4 π r 2 d r = 6 α π R ∫ 0 R / 2 r 3 d r

Q 1 = 6 α π R r 4 4 | R 2 0 = 6 α π R R 4 64

Portanto:

Q 1 = 3 32 α π R 3

Para R / 2 ≤ r ≤ R :

Q 2 = ∫ ρ d V = ∫ R 2 R α 1 - r R 2 4 π r 2 d r

Ou seja:

Q 2 = 4 π α ∫ R 2 R r 2 - r 4 R 2 d r = 4 π α r 3 3 - 1 R 2 r 5 5 | R R / 2

Substituindo o intervalo de integração:

Q 2 = 4 π α R 3 3 - R 3 5 - R 3 24 - R 3 160 = 4 π α R 3 7 24 - 31 160

Q 2 = π α R 3 7 6 - 31 40 ∴ Q 2 = 47 120 π α R 3

E, para r ≥ R :

Q 3 = ρ V = 0

Portanto, a carga total será dada por:

Q = Q 1 + Q 2 + Q 3 = 3 32 α π R 3 + 47 120 π α R 3 + 0

Q = 45 + 188 480 π α R 3 = 233 480 π α R 3

E:

α = 480 233 π R 3 Q

Passo 2

Agora, para cada região, vamos verificar a carga total que é envolvida de acordo com a distância r e determinar o campo elétrico da respectiva região a partir da lei de Gauss que é dada por:

Φ = E A = Q T ϵ 0

Logo, para r ≤ R / 2 , a carga total envolvida é Q 1 = ρ 1 V 1 . Então:

E 1 4 π r 2 = 1 ϵ 0 6 α π R ∫ 0 r r 3 d r

E 1 = 1 4 π r 2 ϵ 0 6 α π R r 4 4 → E 1 = 6 16 R ϵ 0 α r 2

Substituindo o valor de α :

E 1 = 6 16 R ϵ 0 480 233 π R 3 Q r 2

Então:

E 1 = 180 233 π ϵ 0 R 4 Q r 2

Da mesma forma, a região R / 2 ≤ r ≤ R envolve as cargas Q 1 e Q 2 :

E 2 4 π r 2 = Q 1 + Q 2 ϵ 0 = 3 32 ϵ 0 α π R 3 + 1 ϵ 0 4 π α r 3 3 - 1 R 2 r 5 5 | r R / 2

Então:

E 2 4 π r 2 = 3 32 ϵ 0 α π R 3 + 1 ϵ 0 4 π α r 3 3 - r 5 5 R 2 - R 3 24 - R 3 160

E 2 4 π r 2 = 3 32 ϵ 0 α π R 3 + 1 ϵ 0 4 π α r 3 3 - r 5 5 R 2 - 17 R 3 480

Encontrando o MMC de todos os termos:

E 2 = α π R 3 480 ϵ 0 4 π r 2 45 + 640 r R 3 - 384 r R 5 - 68

E 2 = α π R 3 480 ϵ 0 4 π r 2 640 r R 3 - 384 r R 5 - 23

E, substituindo α , o resultado final para essa região pode ser dado por:

E 2 = 480 233 π R 3 Q α π R 3 480 ϵ 0 4 π r 2 640 r R 3 - 384 r R 5 - 23

Ou seja:

E 2 = 1 233 Q k r 2 640 r R 3 - 384 r R 5 - 23

Por último, para a região r ≥ R , a carga total envolveida é a soma das cargas nas três regiões. Então:

E 3 4 π r 2 = Q 1 + Q 2 + Q 3 ϵ 0 = 1 ϵ 0 Q 1 + Q 2 + ρ 3 V 3

Mas como ρ 3 é zero, então só resta a soma dos outros dois termos:

E 3 = 1 ϵ 0 4 π r 2 233 480 π α R 3 = k r 2 233 480 π R 3 480 233 π R 3 Q

∴ E 3 = k Q r 2

Passo 3

Para calcularmos a quantidade da carga total Q que se encontra dentro da região R / 2 ≤ r ≤ R , Q 2 , vamos aproveitar os resultados obtidos no Passo 1 , tal que essa quantidade é dada por:

Q 2 Q = 47 120 π α R 3 233 480 π α R 3 = 47 120 480 233 = 188 233

Que representa aproximadamente:

Q 2 = 80 , 7   %   d e   Q

Passo 4

Para calcular o campo elétrico em r = R / 2 , podemos utilizar tanto a equação para r ≤ R / 2 ou para R / 2 ≤ r ≤ R , visto que ambas possuem mesmo resultado na fronteira. Dessa forma, utilizando E 1 :

E 1 = 180 233 π ϵ 0 R 4 Q R 2 2 = 45 233 π ϵ 0 R 2 Q

E agora, usando E 2 :

E 2 = 1 233 Q k R 2 2 640 R 2 R 3 - 384 R 2 R 5 - 23

E 2 = 4 233 k Q R 2 640 1 8 - 384 1 32 - 23 = 4 233 Q R 2 1 4 π ϵ 0 45

Portanto:

E 2 = 4 5 233 π ϵ 0 Q R 2

Passo 5

Devemos lembrar, agora, que a força do movimento harmônico simples é diretamente proporcional a distância r percorrida na oscilação e é dada por:

F M H S = - k r

Além disso, a força elétrica gerada por um campo elétrico é dada por:

F = q E

No entanto, para que a força resulte em um movimento harmônico simples, ela requer que o campo elétrico seja diretamente proporcional ao deslocamento da oscilação r , o que não ocorre em nenhuma das três regiões.

Logo, o movimento é oscilatório, devido a carga do elétron ser negativa e isso resultar numa força negativa, ou seja, numa força atrativa (isso faz com que a força seja atraída para o centro da esfera causando a oscilação), mas não é harmônico simples.

Resposta

a   480 233 π R 3 Q

b   r ≤ R 2 → 180 233 π ϵ 0 R 4 Q r 2

R 2 ≤ r ≤ R → 1 233 Q k r 2 640 r R 3 - 384 r R 5 - 23

r ≥ R → k Q r 2

c   188 233 = 0 , 80 7

d   45 233 π ϵ 0 R 2 Q

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma esfera oca condutora com raio interno a e raio externo b possui uma carga puntiforme positiva Q , localizada em seu centro. A carga total sobre a esfera oca é igual a - 3 Q e está isolada de suas
Uma esfera dentro de uma esfera. Uma esfera condutora sólida de raio a possui carga q . Ela está no interior de uma esfera condutora oca concêntrica com raio interno b e raio externo c . A esfera cond
Um cilindro sólido muito longo de raio R possui uma distribuição uniforme de carga positiva, sendo ρ a carga por unidade de volume. a Deduza uma expressão para o campo elétrico no interior do volume,
O cabo coaxial. Um cabo coaxial longo é constituído por um cilindro interno condutor de raio a e por um cilindro externo coaxial com raio interno b e raio externo c . O cilindro externo está apoiado e
Um tubo cilíndrico condutor muito longo (cilindro oco) possui raio interno a e raio externo b . Ele possui carga por unidade de comprimento igual a + α , em que α é uma constante positiva com unidades