Duas bolas são atiradas com a mesma rapidez do topo de um penhasco de altura . Uma bola é atirada a um ângulo acima da horizontal. A outra bola é atirada a um ângulo abaixo da horizontal. Mostre que cada bola atinge o chão com a mesma rapidez e encontre esta rapidez em termos de h e da rapidez inicial (Ignore a resistência do ar.)
Passo 1
E aí pessoal, beleza? Vamos lá provar esse experimento. A figura do problema nos ajuda a visualizar melhor a situação:
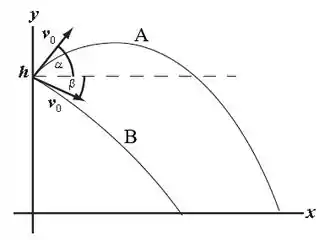
O enunciado quer que mostremos que as bolas atingem o chão com a mesma velocidade. Bom, sabemos que o módulo da velocidade é dado por:
Então vamos encontrar os valores de e . Para temos:
Para temos que:
Como temos que:
Passo 2
Agora vamos substituir os valores que encontramos:
Mas se a gente observar direitinho temos que:
Então podemos escrever:
Observe que a velocidade final de chegada ao solo , só depende da velocidade inicial de lançamento e da altura do ponto de início ao fim.