Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 21.1 - Ex. 47

Duas cargas puntiformes, cada uma com carga q , estão na base de um triângulo equilátero cujos lados têm comprimento L , como mostra a figura 21-38. Uma terceira carga puntiforme tem carga igual a 2 q e está no ápice do triângulo. Onde deve ser colocada uma carga puntiforme q para que o campo elétrico no centro do triângulo seja igual a zero? (O centro está no plano do triângulo e equidistante dos três vértices)

Passo 1

Vamos adotar um sistema de coordenadas x y como mostra a figura:

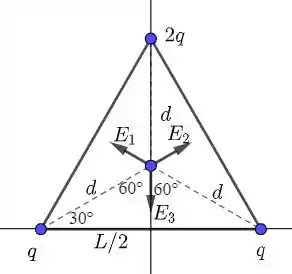
Veja que a resultante entre E → 1 e E → 2 estará apontando verticalmente para cima, pois

E 1 = E 2 = k q d 2

onde

d = L / 2 sen ⁡ 60 ° = 3 3 L

Ou seja,

E 1 = E 2 = 3 k q L 2

Dessa forma, a resultante de E 1 e E 2 será:

E 12 = 2 E 1 cos ⁡ 60 ° = 3 k q L 2

Além disso, o campo elétrico devido a carga 2 q é:

E 3 = k 2 q d 2 = 6 k q L 2

Passo 2

Assim, o campo resultante será:

E r = E 12 - E 3 = 3 k q L 2 - 6 k q L 2 = - 3 k q L 2

Ou, em termos vetoriais,

E → r = - 3 k q L 2 y ^

Assim, devemos colocar uma carga q , positiva, abaixo do centro (para ela criar um campo para cima):

3 k q L 2 = k q y 2

Ou seja,

y = L 3 = 3 L 3

Resposta

Devemos colocar a carga a uma distância 3 L 3 abaixo do centro.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas pequenas esferas de alumínio, cada qual com uma massa igual a 0,0250 kg, estão separadas por uma distância de 80,0 cm.Quantos elétrons estão presentes em cada esfera? (O número atômico do alumíni
Duas pequenas esferas de plástico possuem cargas elétricas positivas. Quando estão separads por uma distância iguala 15 cm, a força de repulsão entre elas possui módulo igual a 0,220 N. Qual será a a
Uma pequena esfera de chumbo de massa igual a 8,0 g possui excesso de elétrons com uma carga líquida igual a –3,2x10 - 9 C. Quantos elétrons em excesso existem por atômo de chumbo? O número atômico do
Duas pequenas esferas separadas a uma distância igual a 20,0c m possuem cargas iguais. Quantos elétrons em excesso devem estar presentes em cada esfera para que o módulo da força de repulsão entre ela
Duas pequenas esferas de plástico possuem cargas elétricas positivas. Quando estão separadas por uma distância igual a 15c m , a força de repulsão entre elas possui módulo igual a 0,220N . Qual será a