Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 29.Exercícios e Problemas - Ex. 67
Duas cargas puntiformes positivas q, estão localizadas sobre o eixo y em
a. Obtenha uma expressão para o potencial criado pelas cargas ao longo do eixo x.
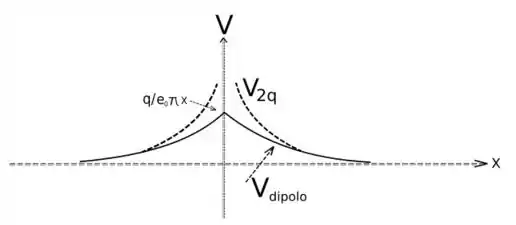
b. Desenhe o gráfico de V versus x para a região . Para comparação, trace uma linha pontilhada para indicar o potencial criado uma carga puntiforme 2q posicionada na origem do sistema de coordenadas.
Passo 1
Fala galera, tudo tranquilo? Deixarei um esquema abaixo sobre como é elaborado este problema de dipolo.
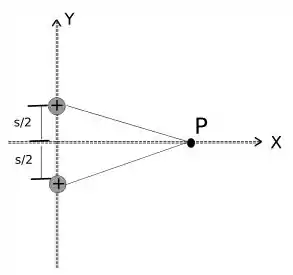
Podemos encontrar a distância d até o ponto P por meio de pitágoras.
e
Agora podemos expressar cada potencial separadamente com respeito ao ponto P, potencial da partícula 1 em relação a P e potencial da partícula 2 em relação a P.
,
O potencial do dipolo pode ser expressado como
.
Passo 2
Agora para o item (b) precisamos esboçar um gráfico do potencial em função da distância. Primeiro perceba que o potencial é dado em função de , se colocarmos x em evidência, a equação para o potencial do dipolo fica com a seguinte expressão:
, para grandes distâncias , a equação do denominador se resume ao valor 1 e temos o mesmo potencial para ambos os lados
Resposta
(a)
(b)
