Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 1.Problemas - Ex. 51

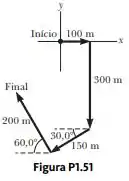
Uma pessoa que vai fazer uma caminhada segue o trajeto mostrado na Figura P1.51. A viagem total é composta por quatro trajetórias em linha reta. No final da caminhada, qual é o deslocamento resultante da pessoa medido a partir do ponto de partida?

Passo 1

Eai galera! Belezinha? Vamos resolver mais uma questão?

Neste exercício vamos colocar todos os vetores saindo da origem, será mais fácil para encontrar o deslocamento resultante. Inicialmente temos que fazer a decomposição dos vetores que estão inclinados no sistema cartesiano, são eles os vetores deslocamento de 150   m e 200   m . Para facilitar vamos nomear os vetores em A → , B → , C → e D → .

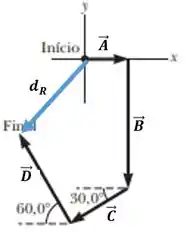
Representando os vetores e suas decomposições no plano cartesiano, podemos fazer o somatório das forças nos eixos.

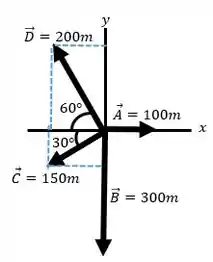
Para C → :

C x → = C → . cos ⁡ 30 ° = 150 . 3 2 = 75 3   m = 130   m

C y → = C → . sen ⁡ 30 ° = 150 . 1 2 = 75   m

Para D → :

D x → = D → . cos ⁡ 60 ° = 200 . 1 2   = 100   m

D y → = D → . sen ⁡ 60 ° = 200 . 3 2 = 100 3 = 173   m

Passo 2

Representando os vetores e suas decomposições no plano cartesiano, podemos fazer o somatório das forças nos eixos.

∑ F x = - D x → - C x → + A → = 0

∑ F y = D y → - C y → - B → = 0

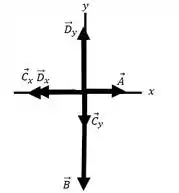
Substituindo a Força em x .

∑ F x = - 130 - 100 + 100 = - 130   m

Substituindo a Força em y .

∑ F y = 173 - 75 - 300 = - 202   m

Passo 3

A representação do vetor resultante

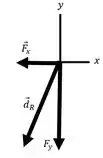
Como temos dois vetores perpendiculares precisamos aplicar o Teorema de Pitágoras para encontrar o deslocamento resultante.

d R = F x 2 + F y 2  

d R = - 130 2 + - 202 2  

d R = 16900 + 40804  

d R = 240   m

Passo 4

Cálculo do ângulo com o eixo x positivo.

sen ⁡ θ = 202 240

sen ⁡ θ = 0,84

θ - 1 = a r c s e n   0,84

θ = 57 °

O ângulo formado pelo eixo x positivo até o vetor deslocamento resultante é

α = 180 + 57 = 237 °

Resposta

d R = 240   m , α = 237 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um jogador de golfe precisa de três tacadas para colocar a bola no buraco. A primeira tacada lança a bola 3,66m para o norte, a segunda 1,83m para sudeste e a terceira 0,91m para sudoeste . Determine
As dimensões de uma sala são 3,00 (altura) × 3,70m × 4,30m . Uma mosca parte de um canto da sala e pousa em um canto diagonalmente oposto. (a) Qual é o módulo do deslocamento da mosca? (b) A distância
O vetorA → tem um módulo de 12,0m e faz um ângulo de 60,0 ° no sentido anti-horário com o semieixox positivo de um sistema de coordenadas x y . O vetor B → é dado por 12,0m i →+8,00m j → no mesmo sist
Determine a soma dos quatro vetores a seguir (a) em termos dos vetores unitários e em termos (b) do módulo e (c) do ângulo em relação ao semieixo x positivo. p → = 10,0 m ,25,0 °s e n t i d oa n t i -
Se B → é somado a A → , o resultado é 6 ,0 i ^ + 1 ,0 j ^ . Se B → é subtraído de A → , o resultado é - 4,0 i ^+ 7,0 j ^ . Qual é o módulo de A → ?