Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 1.Problemas - Ex. 55
Uma topógrafa mede a largura de um rio em linha reta pelo método a seguir (Fig. P1.55). Começando diretamente em frente a uma árvore na margem oposta, ela anda m ao longo da margem para estabelecer uma referência. Então, avista a árvore. O ângulo da referência até a árvore é . Qual é a largura do rio?
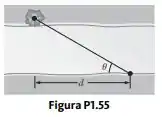
Passo 1
Aqui a gente só vai precisar aplicar relações trigonométricas. Você deve lembrar das 3 relações fundamentais, que são seno, cosseno e tangente.
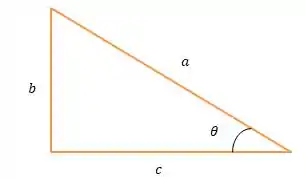
Com isso, a gente tem:
Passo 2
Se o objetivo é determinar a largura do rio (que nesse triângulo desenhado de cima equivaleria ao lado ), precisamos usar alguma relação que contenha .
Nesse caso, poderiam ser: ou .
Só que o exercício nos dá a distância , que no triângulo desenhado equivaleria ao lado . Então, vamos usar a relação tangente, em que:
Assim, nossa única incógnita vai ser , equivalente à largura do rio, que calculamos bem facilmente: