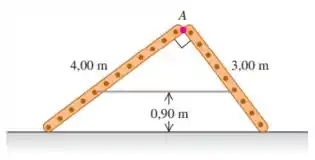
Duas escadas, uma de 4,00 m e outra de 3,00 m de comprimento, estão articuladas em um ponto A e ligadas entre si por uma corda horizontal situada a 0,90 m acima do solo (Figura P11.89). As escadas pesam 480 N e 360 N, respectivamente, e o centro de gravidade de cada uma se localiza em seu respectivo centro. Suponha que o piso esteja encerado e sem atrito. (a) Ache a força de baixo para cima na parte inferior de cada escada. (b) Ache a tensão na corda. (c) Ache o módulo da força que uma escada exerce sobre a outra no ponto A. (d) Supondo que um pintor com 800 N esteja em pé sobre o ponto A, calcule a tensão na corda horizontal.
Passo 1
E aiiiiiiiii galera, tudo bom com vocês?
Vamos fazer mais uma questão!!
Bom... o enunciado nos dá a seguinte figura:
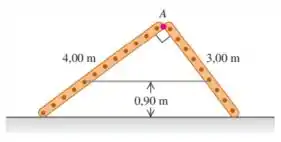
Temos duas escadas que estão articuladas em um ponto A e ligadas entre si por uma corda horizontal situada aacima do solo.
As escadas pesam e , respectivamente, e o centro de gravidade de cada uma se localiza em seu respectivo centro.
Queremos encontrar a força de baixo para cima na parte inferior de cada escada, a tensão na corda e o módulo da força que uma escada exerce sobre a outra no ponto A.
Por fim, supondo que um pintor com esteja em pé sobre o ponto A, queremos calcular a tensão na corda horizontal.
Passo 2
Letra a:
Pegando os torques sobre a extremidade direita:
Então,
pode ser encontrado de maneira semelhante, ou a partir de
Passo 3
Letra b:
A tensão na corda pode ser encontrada encontrando o torque em cada escada, usando o ponto A como a origem. O braço de alavanca da corda é 1,50 m. Para a escada da esquerda:
Então,
Para conferir, usando os torques na escada da direita, temos:
Que nos dá o mesmo resultado.
Passo 4
Letra c:
O componente horizontal da força em A deve ser igual à tensão encontrada no item (b). A força vertical deve ser igual em magnitude à diferença entre o peso de cada escada e a força na parte inferior de cada escada, . A magnitude da força em A é então:
Passo 5
Letra d:
A maneira mais fácil de fazer isso é ver se a carga adicionada será distribuída no chão de tal forma que
E
Assim, chegamos na tensão :