Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 10.1 - Ex. 42

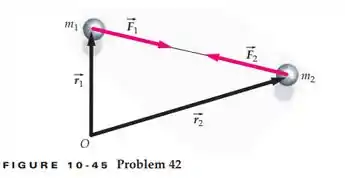
(a) Duas estrelas, de massas m 1 e m 2 , estão localizadas em r 1 → e r 2 → em relação a uma origem O , como mostrado na Figura 10-45. Elas exercem, uma sobre a outra, forças de atração gravitacional iguais e opostas. Para este sistema de estrela dupla, determine o torque resultante exercido por estas forças internas em relação à origem O e mostre que ele vale zero apenas se as duas forças estão sobre a mesma linha que liga as partículas. (b) O fato de que forças de pares da terceira lei de newton não são apenas iguais e opostas, mas estão, também, sobre a mesma linha que liga os dois corpos, é às vezes chamado de forma forte da terceira lei de Newton. Por que é importante adicionar a ultima frase? Dica: Considere o que aconteceira a estes dois corpos se as forças estivessem afastadas uma da outra.

Passo 1

Repare que cada força gera torque na a qual esta atuando. Esse torque é feito com relação a um eixo perpendicular ao papel passando pelo ponto O !! O torque resultante vai ser o seguinte:

τ r e s → = r 1 → × F 1 → + r 2 → × F 2 →

Pela terceira lei de Newton:

F 1 → = - F 2 →

Logo,

τ r e s → = r 1 → × - F 2 → + r 2 → × F 2 → = r 2 → - r 1 → × F 2 →

O vetor r 2 → - r 1 → é o vetor que liga as duas estrelas. Assim, ele está na mesma direção de F 2 → .

τ r e s → = 0

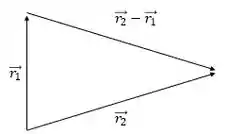
Passo 2

Agora vamos lembrar de uma coisa!

τ r e s → = r 12 → × F 2 →

Tirando o modulo:

τ r e s → = r 12 → ⋅ F 2 → ⋅ s e n ( θ )

Onde θ é o ângulo entre os vetores r 12 → e F 2 → !!

Passo 3

Se as forças não estão sobre a mesma linha (não tem a mesma direção), então o torque será diferente de zero, pois do produto vetorial A → × B → = A → ⋅ B → ⋅ s e n ( θ ) esse θ deixa de ser diferente de zero. Esse torque resultante pode causar uma aceleração angular no sistema, contrario a observação, e não fazendo sentido fisicamente!!

Resposta

(a)   τ r e s → = 0

(b) Se as forças não estão sobre a mesma linha (não tem a mesma direção), então o torque será diferente de zero, pois do produto vetorial A → × B → = A → ⋅ B → ⋅ s e n ( θ ) esse θ deixa de ser diferente de zero. Esse torque resultante pode causar uma aceleração angular no sistema, contrario a observação, e não fazendo sentido fisicamente!!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

12.20. Na figura EX12.20, qual é o torque resultante em torno do centro de massa?
44. A força F → = - 10 j ^N é exercida sobre uma partícula localizada em r → = 5 i ^ + 5 j ^ m . Qual é o torque sobre a partícula em torno da origem?
45. A força F → = - 10 i ^ + 10 j ^ N é exercida sobre uma partícula localizada em r → = 5 j ^m . Qual é o torque sobre a partícula em torno da origem?
Os halteres da FIGURA Q12.9 são todos de mesmo tamanho, e as forças exercidas têm todas o mesmo módulo. Ordene em sequência decrescente os valores absolutos dos torques de τ a , τ b e τ c . Explique o
Seis forças são exercidas na porta da FIGURA Q12.8. Ordene em sequência decrescente os módulos dos seis torque de τ a a τ f em torno da dobradiça. Explique o seu ordenamento.