Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 12.Questões Conceituais - Ex. 9
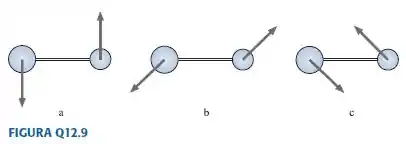
Os halteres da FIGURA Q12.9 são todos de mesmo tamanho, e as forças exercidas têm todas o mesmo módulo. Ordene em sequência decrescente os valores absolutos dos torques de , e . Explique o seu ordenamento.
Passo 1
Olá, tudo bem? Para resolver essa questão precisamos lembrar-nos de como se calcula o torque:
Onde é o braço e alavanca, é a força aplicada e é o ângulo entre o braço de alavanca e a força.
De cara vemos que o maior torque é o , pois o ângulo entre a força e o braço de alavanca é , e assim temos o torque máximo que essa força pode produzir. Esse torque é .
Passo 2
Agora vamos aos outros torques. O ângulo entre o braço de alavanca e a força no desenho é , então o torque produzido por essa força seria:
Já o ângulo no desenho é , mas aqui usamos uma identidade trigonométrica:
Então temos que esse torque também vai ser .
Esses dois torques são iguais, e valem, necessariamente, um valor absoluto menor do que , pois tem seu valor máximo em .
Passo 3
Então em ordem decrescente temos:
Beleza?
Espero ter ajudado!
Vamos pra próxima?