Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 33.1 - Ex. 59

Duas fontes de luz com comprimentos de ondas iguais a 700   n m estão separadas por uma distância horizontal x . Elas estão a 5.00   m de uma fenda vertical de largura 0.500   m m . Qual é o menor valor de x para o qual o padrão de difração das fontes possa ser resolvido pelo critério de Rayleigh?

Passo 1

SIMBORA PARA MAIS UMA, aumenta o som da playlist, dá um gole de água e me acompanhe; Galera, nessa aqui podemos usar o critério de Rayleigh para fendas e a geometria do diagrama abaixo que mostra os padrões de difração sobrepostas para expressar x em termos de L , λ , e a largura a da fenda, te liga no diagrama:

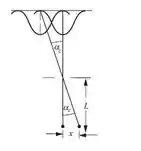
Com isto estabelecido, vamos para os problemas!

Passo 2

Bem, de acordo com o diagrama:

α c ≈ x L

Para fendas, o critério de Rayleigh é:

α c = λ a

Igualando as duas equações, temos:

x L =   λ a

x =   λ   L a

Substituindo as variáveis por valores numéricos, obtemos:

x =   700   n m ( 5.00   m ) 0.500   m m

x =   7.00   m m

VENCEMO, é isso aí, até a próxima galera, fiquem bem!

Resposta

x =   7.00   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Luz com comprimento de onda igual a 700n m incide em um orifício com diâmetro de 0.100m m . (a) Qual é o ângulo entre o máximo central e o primeiro mínimo de difração para o padrão de difração de Frau
O teto de seu quarto de leitura provavelmente seja coberto com telha acústica, que tem pequenos orifícios separados por aproximadamente 6.00m m . (a) Usando luz com comprimento de onda de 500n m , a q
A estrela Mizar na Ursa Maior é o sistema binário de estrelas que têm magnitudes aproximadamente iguais. A separação angular entre as duas estrelas é 14 segundos de arco. Qual é o diâmetro mínimo da p
Duas fontes de luz com comprimentos de onda iguais a 700n m estão a 10.0m de distância do orifício do Problema 57. Qual deve ser a separação entre as fontes para que seus padrões de difração sejam res