Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 33.1 - Ex. 62
A estrela Mizar na Ursa Maior é o sistema binário de estrelas que têm magnitudes aproximadamente iguais. A separação angular entre as duas estrelas é segundos de arco. Qual é o diâmetro mínimo da pupila que permite a resolução das duas estrelas usando luz com comprimento de onda de ?
Passo 1
FALA GALERA, salve, salve, firmeza, firmeza (bossa nova tocando no fundo, porque o responde aí também é cultura). Para essa questão, podemos utilizar o critério de Rayleigh para aberturas circulares e a geometria do diagrama abaixo para obter uma expressão, na qual podemos calcular o valor do diâmetro mínimo da pupila que permite a resolução das estrelas binárias. Observe o diagrama:
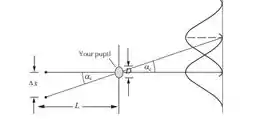
Com isso estabelecido, agora vamos resolver esse problema de vez, hehe.
Passo 2
Utilizando a definição do critério de Rayleigh, podemos obter:
Aplicando os valores numéricos na equação, temos:
E dessa forma, me despeço, questão feita com sucesso! Até a próxima pessoal, Love u all!