Exercícios de Resolução e Dispersão de uma Rede de Difração - Lista de Exercícios Resolvida

Uma rede de difração tem uma resolução .

1. Mostre que a diferença de frequências que se encontra no limite da resolução, , é dada por .
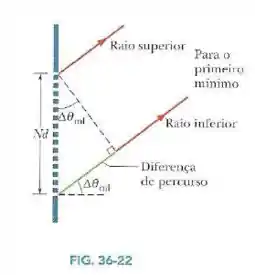
2. Para a Fig. 36-22, mostre que a diferença entre os tempos de percurso do raio de baixo e do raio de cima é dada por .
3. Mostre que e, portanto, esse produto não depende dos parâmetros da rede. Suponha que .

A luz de uma lâmpada de sódio, com um comprimento de onda , incide perpendicularmente em uma rede de difração com em de largura.

Determine a Dispersão da rede em segunda ordem.

Mostre que a dispersão de uma rede de difração é dada por:

Um feixe luminoso contém dois comprimentos de onda, e , que devem ser resolvidos com uma rede de difração.

Se a largura da rede é , qual é o número mínimo de linhas necessário para que os dois comprimentos de onda sejam resolvidos em segunda ordem?

Um feixe luminoso que contém uma faixa estreita de frequências em torno de incide perpendicularmente em uma rede de difração com uma largura de e uma densidade de linhas de .

Para essa luz, qual é a menor diferença de comprimentos de onda que a rede é capaz de resolver em terceira ordem?

A luz de uma lâmpada de sódio, com um comprimento de onda , incide perpendicularmente em uma rede de difração com em de largura.

Determine a Dispersão da rede em segunda ordem.

A luz proveniente de um arco de ferro possui diversos comprimentos de onda.

Dois entre eles são e .

Você deseja separar essas duas linhas espectrais na primeira ordem usando uma rede com de comprimento.

Qual é o menor número de fendas por centímetro que essa rede deve possuir?

6. Nenhuma das anteriores

Uma rede de difração tem linhas. Radiação luminosa contendo ondas de dois comprimentos de onda e incidem perpendicularmente nessa rede.

É possível resolver estes dois comprimentos de onda sabendo-se que a máxima ordem de difração que pode ser observada para é oito?

a) Em um experimento de fenda dupla, a abertura de cada fenda vale e distância entre as fendas é . Incide-se luz de comprimento e onda de perpendicularmente ao plano das fendas. Faça um gráfico da intensidade da luz em função de , sendo o ângulo de chegada dos raios no anteparo, em relação ao eixo central, incluindo ao menos as envoltórias até os segundos mínimos de difração. Dentro da envoltória central de difração, ache o valor das intensidades máximas dos picos de interferência, relativos àquela para .

b) Uma rede de difração tem o espaçamento entre fendas igual a . Ache a dispersão da rede em máximos de 1ª ordem e assim encontre a abertura angular entre comprimentos de onda incidentes de e . Para, nessas condições, ser capaz de resolver esses comprimentos de onda, qual deve ser o número mínimo de fendas da rede?

Deseja-se construir um espectrômetro de rede que permita separar luz violeta () da luz azul () em ordem. Qual é o número mínimo de fendas necessárias para a separação?

Complete a frase corretamente e justifique:

Quanto maior é a dispersão de uma rede de difração:

(a ) Maior é a distância entre as linhas produzidas por diferentes comprimentos de onda.

(b ) Mais estreitas são as linhas na figura de difração.

(c ) Mais largas são as linhas na figura de difração.

(d ) Menor é a distância entre as linhas produzidas por diferentes comprimentos de onda.

(e ) Maior é a resolução da rede.

Escolha a resposta correta e justifique: Uma rede de difração comum não pode ser usada para experimentos de difração de raiosX porque:

(a ) A maioria dos materiais dessas redes não difrata raios X.

(b ) A resolução das redes de difração comuns é insuficiente no caso de raios X.

(c ) Raios X não são luz visível.

(d ) A distância entre as linhas das redes comuns é bem maior que o comprimento de onda dos raios X.

A luz de uma lâmpada com comprimento de onda de 550 nm, incide perpendicularmente em uma rede de difração com 50000 ranhuras por 10 cm de largura.

(a ) Determine a Dispersão (D) da rede em segunda ordem e obtenha a resolução dessa rede em quarta ordem.

(b ) Calcule a meia largura do máximo principal central formado por essa rede.

Considere que a placa seja substituída por uma rede de difração de 1,0 cm de comprimento, com fendas bastante mais estreitas, mas com o mesmo espaçamento anterior de 4,90µm. Sobre a rede, incide-se perpendicularmente luz com comprimentos de onda dentro do espectro do visível, de 400 a 700 .

(d) Para comprimentos de onda na região do amarelo (λ∼550nm), qual é a menor variação de comprimento de onda que esta rede consegue resolver, para máximos de 2º ordem?

Um pesquisador quer fabricar uma rede de difração que possa separar dois comprimentos de onda na faixa do azul, e .

a) Qual deve ser a distância entre as fendas sucessivas para que a separação angular entre e seja de para máximos de primeira ordem?

b) Verifique se 200 fendas são suficientes para resolver e em máximos de segunda ordem.

c) Genericamente, para quaisquer comprimentos de onda possam ser distinguidos, explique qualitativamente o critério a ser cumprido.

d) No caso particular da rede de difração, argumente porque a resolução depende do número de fendas e da ordem dos máximos de interferência.

Considere agora que a rede de difração do item anterior tem comprimento total de 3,0 cm e recebe uma luz de comprimento de onda λ = 500 nm.

(c ) Calcule a dispersão que esta rede pode resolver em segunda ordem.

(d ) Encontre a menor diferença de comprimentos de onda que essa rede pode resolver em ordem 2.

A linha D do espectro de Sódio é um dubleto (duas linhas próximas) com comprimentos de onda 𝜆1 = 589 𝑛𝑚 e 𝜆2 = 589,6 𝑛𝑚. Uma rede de difração permite observar esse dubleto no limite da resolução. Mais ainda, a terceira ordem (𝑚 = 3) possui um ângulo de 10° com a normal à tela de observação. Determine:

(a) o espaçamento entre as ranhuras.

(b) o número 𝑁 de ranhuras da rede.

Qual é o menor número de fendas de uma rede de difração para se resolver luz com comprimentos de onda iguais a e e onde só são visíveis os máximos até ordem 3?

Deseja-se construir um espectrômetro de rede que permita separar luz violeta () da luz azul () com o terceiro máximo principal.

Dentre as opções abaixo, qual o número mínimo de fendas são suficientes para essa tarefa?