Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 16.6 - Ex. 39
Duas ondas senoidais de mesmo período, com e de amplitude, se propagam no mesmo sentido em uma corda esticada, onde produzem uma onda resultante com uma amplitude de . A constante de fase da onda de é . Qual é a constante de fase da onda de ?
Passo 1
Vamos então imaginar que o fasor da onda de de amplitude está exatamente em cima do eixo .
E que o fasor da onda de está em algum outro lugar, formando um ângulo com o primeiro fasor.
Vamos desenhar mais ou menos a situação:
Passo 2
Independentemente de qual seja esse ângulo , a amplitude da soma desses dois fasores vai seguir a lei dos cossenos.
Aplicando a regra do paralelogramo:
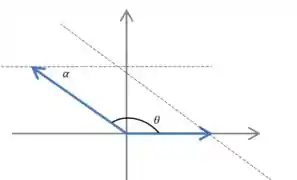
Então tome cuidado! Os ângulos opostos nesse paralelogramo são iguais, mas pra achar a amplitude não podemos aplicar a lei dos cossenos diretamente sobre o , temos que aplicar sobre um dos outros dois ângulos.
Como queremos que a resultante tenha amplitude :
Passo 3
Agora vamos usar isso pra achar o valor de .
Como a soma dos ângulos internos do paralelogramo é :
E essa vai ser a diferença de fase das ondas, e como a constante de fase da primeira onda é zero:
Resposta
A constante de fase é .