Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.8 - Ex. 34

Use um diagrama em escala para determinar os componentes x e y dos vetores seguintes. Para cada vetor, os números indicam o módulo do vetor e o ângulo que ele faz com o eixo + O x   medido supondo-se uma rotação no sentido do eixo + O x para o eixo + O y . Ache para a) módulo 9,3   m ângulo 60,0°; b) módulo 22,0   k m , ângulo 135°; c) módulo   6,35   c m , ângulo 307°.

Passo 1

Fala aí! tudo certinho? 😉

Nesse problema queremos obter as componentes de alguns vetores dados no enunciado.

Lembra como fazemos isso? 👀

Para encontrarmos cada componente basta multiplicar o módulo pelo seno ou cosseno do ângulo.

Lembrando decomposição de vetores:

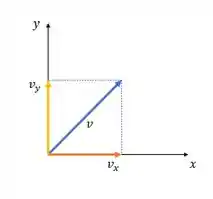
c o s θ = c a t e t o   a d j a c e n t e h i p o t e n u s a = v x v

Assim,

v x = v cos ⁡ θ

E

s e n   θ = c a t e t o   o p o s t o h i p o t e n u s a = v y v

Assim,

v y = v   s e n   θ

Veja só! 😬

Passo 2

No item a) temos um vetor de módulo 9,3   m ângulo 60,0°. Portanto

A x = A · cos ⁡ θ A = 9,3   m ⋅ cos ⁡ 60 °

A x = 4,7 m

A y = A · sin ⁡ θ A = 9,3 m ⋅ sin ⁡ 60 °

A y = 8,1 m

Tranquilo até aqui? 😊

Passo 3

No item b) temos um vetor com módulo 22 k m e ângulo 135 °

B x = B · cos ⁡ θ B = 22 k m �� cos ⁡ 135 °

B x = - 15,6 k m

B y = B · sin ⁡ θ B = 22 k ⋅ sen ⁡ 135 °

B y = 15,6 k m

Bacana, não é? 😁

Passo 4

E por último, temos um vetor com modulo de 6,35 c m e ângulo 307 ° .

C x = C · cos ⁡ θ C = 6,35 c m ⋅ cos ⁡ 307 °

C x = 3,82 c m

C y = C · sin ⁡ θ C = 6,35 ⋅ sen ⁡ 307 °

C y = - 5,7 c m

Tudo certo? 👀

Passo 5

Vamos ilustrar os vetores que calculamos:

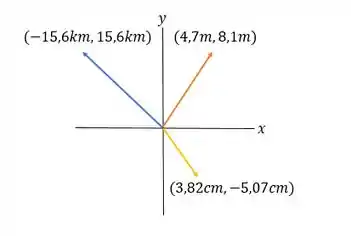
E aí! entendeu tudo? Responde Aí! 😉

Resposta

  1. 4,7 m , 8,1 m
  2. - 15,6 k m , 15,6 k m
  3. 3,82 c m , - 5,07 c m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em uma operação de montagem ilustrada na Figura P1.49, um robô move, primeiro, um objeto em linha reta para cima e, depois, também para o leste, em torno de um arco formando um quarto de um círculo de
Três vetores deslocamento de uma bola de croquet são mostrados na Figura P1.44, em que | A → |=20,0 unidades, | B → | =40,0 unidades e | C → | =30,0 unidades. Encontrea) a resultante em notação de vet
O vetor A → tem componentes x , y e z de 8,00 , 12,00 e – 4,00 unidades, respectivamente.a) Escreva uma expressão de vetor para A → em notação de vetor unitáriob) Obtenha uma expressão de vetor unitár
Dados os vetores A →=2,00i ^+6,00j ^ e B →=3,00i ^–2.00j ^ a) desenhe a soma vetorial C →=A →+ B → e a diferença vetorial D →=A →– B → b) Calcule C → e D → nos termos de vetores unitáriosc) Calcule C
Um controlador de tráfego aéreo observa duas aeronaves na tela de seu radar. A primeira está a uma altitude de800m , a uma distância horizontal de 19,2k m e 25,0 ° a sudoeste. A segunda aeronave está