Um empregado do serviço postal dirige um caminhão de entrega e faz o trajeto indicado na Figura 1.33. Use o método dos componentes para determinar o módulo, a direção e o sentido do deslocamento resultante. Mediante um diagrama vetorial (aproximadamente em escala), mostre que o deslocamento resultante obtido com este diagrama concorda aproximadamente com o resultado obtido pelo método dos componentes.
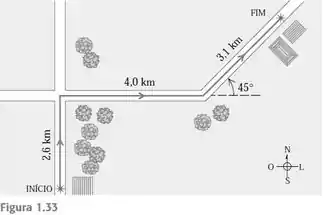
Passo 1
Belezoca pessoal, vamos encontrar a soma vetorial dos três deslocamentos dados na figura:
Primeiro, vamos definir nossas coordenadas. Como temos o motorista se deslocando somente para a direita e para cima, vamos utilizar:
Veja só! 👀
Passo 2
Irado, agora vamos desenhar esse trajeto em vetores, fica desse jeito ó:
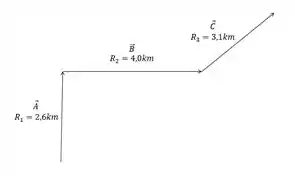
Nesse caso, temos que os deslocamentos são dados como:
Então vamos somar os deslocamento em (horizontal), de forma que:
Calculando cada item dessa somatória temos que:
Portanto, a resultante total na horizontal é dada por:

Tranquilo até aqui? 😬
Passo 3
E o deslocamento em (vertical), da mesma maneira, será dado pelo somatória dos deslocamento na vertical, tal que:
Calculando cada item dessa somatória temos que:
Portanto, a resultante total na vertical é dada por:
Isso quer dizer que o vetor deslocamento total pode ser expresso como:

Bacana, não é? 😉
Passo 4
Show de bolinhas!
Como já conhecemos as componentes em e , vamos calcular o modulo para encontrar o vetor resultante , de modo que o módulo de é dado como:
Logo:
Portanto:

Estamos quase lá! 😁
Passo 5
Vamos calcular a direção do vetor :
Sabemos que para isso, vamos utilizar a relação:
Tal que:
Então substituindo os valores que descobrimos, obtemos:
E colando essas informações em um diagrama, temos que o vetor está disposto de uma forma que:
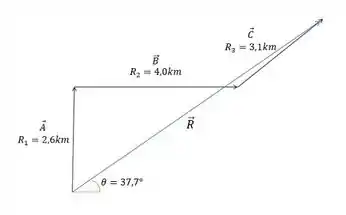
Prontinho! O que achou? Responde Aí! 😎