Enunciado
Física - Young and Freedman - Vol 2- Ed: 14º - Capítulo 12.Exercícios - Ex. 8
Duas massas pontuais, uma de 8,00 kg e outra de 12,0 kg, são mantidas fixas a 50,0 cm de distância. Uma partícula de massa m é solta de um ponto entre as duas massas a 20,0 cm da massa de 8,0 kg ao longo da linha que conecta as duas massas fixas. Ache o módulo, a direção e o sentido da aceleração da partícula.
Passo 1
Faaaaala meu povo, bora iniciar mais um livrinho com a gente!
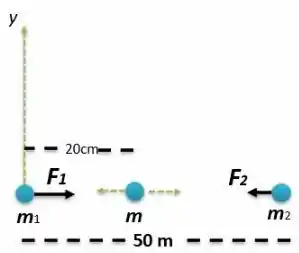
Figura a):
Para essa questão, primeiramente temos que que diagrama de corpo livre é mostrado abaixo para . Temos duas forças gravitacionais exercidas sobre a massa , primeiro é que está entre e e a segunda força está entre e e está na direção oposta de . A força gravitacional é dada pela lei geral da gravidade de Newton por:
Onde é a distância entre e e é dado por e é a constante geral da gravidade e é igual a . Agora basta substituir esses valores na equação, assim encontramos:
Iremos repetir o mesmo passo, mas agora para calcular , teremos:
Passo 2
Como mencionamos acima, as duas forças são exercidas em direções opostas. Assim, a força resultante exercida sobre a massa mm pode ser calculada por:
Essa força é exercida sobre e faz com que ele se mova com uma aceleração . Pela lei do movimento de Newton, essa aceleração pode ser encontrada por:
Substituindo os valores, teremos:
Como mostrado, a partícula se move com aceleração em direção à massa 8 kg.
Tudo certinho? Te vejo na próximaaaaa!