Duas ondas senoidais com a mesma amplitude de e o mesmo comprimento de onda se propagam em uma corda esticada ao longo de um eixo . A onda resultante é mostrada duas vezes na figura, antes e depois que o vale se desloque de uma distância em . A distância entre as marcas do eixo horizontal é ; . A equação de uma das ondas é da forma , onde e cabe ao leitor determinar o sinal que precede . Na equação da outra onda, determine (a) , (b) , (c) , (d) e (e) o sinal que precede .

(b) O número de onda segue a fórmula:

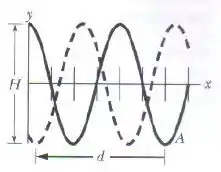
Olhando o gráfico, qual é o comprimento de onda?

Bom, a onda leva quatro “traços” do eixo pra completar uma subida e uma descida, então:

(c) E a frequência angular tem várias formas de calcular ela, mas uma que está mais ao nosso alcance seria:

Uma vez que nós já calculamos o e temos tudo pra calcular o .

O enunciado disse que a onda se desloca em , então:

Sendo assim, será:

(d) O gráfico do enunciado mostra a onda que resulta da soma de outras duas.

O objetivo agora é saber qual era a constante de fase da segunda onda, dado que o da primeira era zero.

Bom, sabemos que a fórmula pra amplitude da onda que vem da soma de outras duas é:

Como a amplitude vai ser metade daquela altura , obtemos que:

Logo:

Então isolando a constante de fase:

Pronto!

(e) O sinal que precede o segue aquele relação importante que você precisa saber:

No nosso caso, a onda se propaga no sentido negativo, então o sinal do é positivo.