Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 11.Problemas Adicionais - Ex. 73

Duas partículas de massa e velocidade se movem em sentidos opostos ao longo de retas paralelas separadas por uma distância de . (a) Qual é o módulo do momento angular do sistema das duas partículas em relação ao ponto médio da distância entre as duas retas? (b) O valor de muda se o ponto em relação ao qual é calculado não está à meia distância entre as retas? Se o sentido de movimento de uma das partículas é invertido, qual é (c) a resposta do item (a) e (d) a resposta do item (b)?

Passo 1

Para iniciar essa questão, vamos observar essa ilustração:

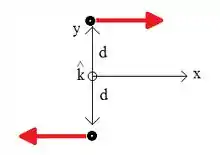
Com essa ilustração podemos usar a regra da mão direita e perceber que, apesar de estarem em sentidos opostos, quando calculamos o momento angular em relação ao eixo , o momento angular de ambos estão no mesmo sentido (). Assim:

Substituindo os valores:

Passo 2

Poderíamos ter estabelecido essa origem em qualquer ponto, tendo em vista que as partículas de mesma massa, distante uma da outra com velocidades no sentido contrário é um “binário” de momento angular, portanto, o momento angular total do sistema sempre será igual ao calculado. (Pode determinar qualquer outro ponto para ser a origem que PRECISA dar o mesmo valor que este).

Passo 3

Neste caso, quando as partículas estão no mesmo sentido, o conceito de “binário” deixa de valer e, então, dependendo do lugar que estabelecemos a origem, teremos valores diferentes. Mantendo a origem onde ilustramos no passo inicial percebemos que:

Porque, agora, um possui o momento angular no sentido e outro no sentido

Resposta

;
;
;
.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula sofre a ação de dois torques em relação à origem: τ 1 → tem módulo de 2 N . m e aponta no sentido positivo do eixo x , τ 2 → tem um módulo de 4 N . m e aponta no sentido negativo do eixo

Uma partícula se move em um plano x y , em torno da origem, no sentido horário, do ponto de vista do lado positivo do eixo z . Em termos dos vetores unitários, qual é o torque que age sobre a partícul

No instante t , o vetor r → = 4 t 2 i → - 2 t + 6 t 2j → fornece a posição de uma partícula de 3 k g em relação à origem de um sistema de coordenadas x y ( r → está em metros e t em segundos). ( a ) E

Uma partícula de 3 , 00kg com uma velocidade de v → = 5 m / s i → - 6 m / s j → está passando pelo ponto x = 3m ,y = 8m . A partícula é puxada por uma força de 7N no sentido negativo do eixo x . Quais

Em um certo instante, a força F → = 4 j → N age sobre um objeto de 0,25 k g cujo vetor posição é r → = 2 i → - 2 k → e cujo vetor velocidade é v → = - 5 i → + 5 k → . Em relação à origem e em termos d