Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 21.4 - Ex. 18a
Duas partículas são mantidas fixas em um eixo . A partícula , de carga , está situada em ; a partícula , de carga , está situada em . A partícula está inicialmente no eixo e é liberada, a partir do repouso, no ponto . O valor absoluto da carga da partícula é . Determine o valor de para que a aceleração inicial da partícula seja (a) no sentido positivo do eixo
Passo 1
Fala ai! Tudo certinho? 😉
Nesse problema temos duas partículas fixas no eixo . A primeira com carga e em e a outra com carga em .
Uma terceira partícula com modulo de carga que está inicialmente sob o eixo em é liberada.
A partir daí temos que determinar o valor de de modo que a terceira partícula acelere no sentido positivo do eixo .
Parece complicado, não é? 🤔
Passo 2
Primeiro, vamos imaginar o que acontece nesse problema:
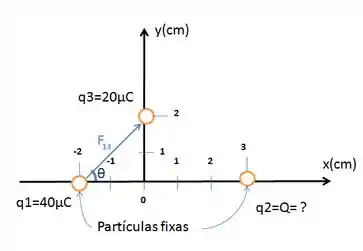
Como a carga é positiva, assim como , elas se repelem com uma força eletrostática que a gente batizou de no desenho.
A letra (a) pergunta qual deve ser o valor de para que a aceleração de esteja no sentido positivo do eixo . Para isso, é necessário que não haja componente de força na direção vertical sobre a partícula . Ok, mas como isso nos ajuda?
Repare que a força na direção vertical sobre só se anulará se a carga for negativa, pois, nesse caso, teremos a seguinte situação:
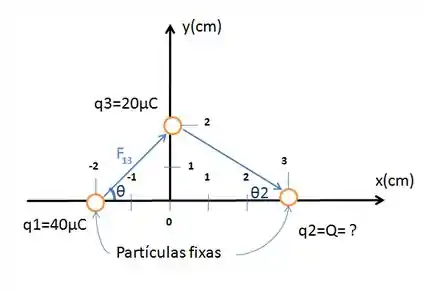
Veja que a componente vertical de está para cima, enquanto a componente de nesse caso, vai estar para baixo e, nesse caso, elas poderão se anular.
Tranquilo até aqui? 😊
Passo 3
Colocando isso na forma de equação, a gente encontra:
Sabemos que pela lei dos senos
Sou seja
Desenvolvendo a equação anterior, a gente encontra o seguinte (após dividir essa equação por ):
Dessa forma, isolando , temos
E aí! Entendeu tudo? Responde Aí! 😉
