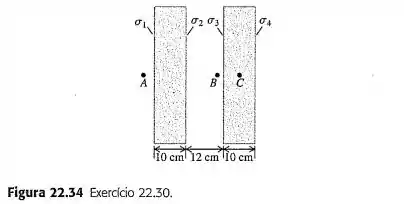
Duas placas de plástico muito grandes e não-condutoras, cada qual com espessura de , carregam densidades de carga uniforme e sobre suas superfícies, como indica a Figura . Essas densidades superficiais de carga possuem os valores , , e . Use a lei de Gauss para determinar o módulo, a direção e o sentido do campo elétrico nos seguintes pontos, afastados das bordas dessas placas: ponto , a da face esquerda da placa à esquerda; ponto , a da superfície interna da placa à direita; ponto , no meio da placa à direita.

Dessa forma, para o ponto que se encontra à esquerda de ambas as placas, temos que o campo gerado pela superfície que tem a densidade negativa irá apontar para a própria superfície ou para a direita (análogo a uma carga puntiforme negativa, cujo campo elétrico gera um fluxo elétrico para dentro). Já as outras partes com densidade superficial positiva irão gerar campos elétricos que apontem para fora (para a esquerda), ou seja, que se “afastem” da própria superfície. Portanto, o campo resultante será dado por:

Substituindo cada campo elétrico:

Logo, o seu resultado é:

Apontando para a esquerda.

Para o ponto que se encontra entre as placas, os campos elétricos gerados pelas superfícies e têm sentidos para a esquerda, direita, esquerda e esquerda respectivamente. Assim:

Portanto:

E também tem sentido para a esquerda.

Em relação ao último ponto que se encontra no meio da placa à direita, os campos elétricos que têm sentido para a esquerda são os das superfícies e , já os que apontam para a direita são das superfícies e . Como a soma dos campos gerados pelas superfícies e é maior, temos:

Portanto:

Com sentido para a esquerda.