Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 33
Durante sua estreia no bungee jumping, seu amigo filma sua queda usando uma câmera. Analisando quadro a quadro, ele descobre que a componente da sua velocidade é (registrada a cada ) da seguinte forma:
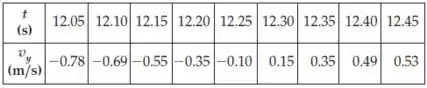
(a) Desenhe um diagrama de movimento. Use-o para encontrar a direção e a magnitude relativa da sua aceleração média para cada um dos oito intervalos de tempo de na tabela. (b) Comente sobre como o sinal componente da sua aceleração varia ou não conforme você inverte o sentido do movimento.
Passo 1
Vamos desenhar alguns vetores que representem cada uma dessas velocidades:
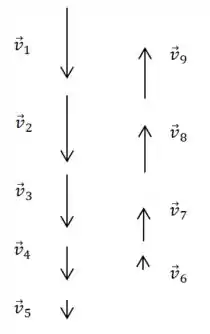
Na verdade todos esses vetores estão sobre a mesma reta, mas desenhamos dessa forma por conveniência. Em todos os intervalos de tempo a aceleração aponta na vertical para cima.
Você pode verificar isso fazendo a diferença de vetores (geometricamente), ou simplesmente observando que a velocidade está sendo “puxada” para apontar nessa direção e sentido.
Passo 2
(b) Para calcular a magnitude da aceleração em cada intervalo vamos ter que usar a seguinte fórmula:
Em todos os casos o intervalo de tempo é , mas os valores de são diferentes. Vamos fazer uma tabela:
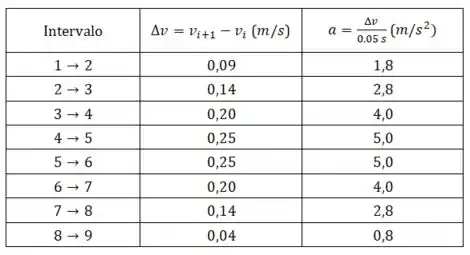
Pela nossa tabela podemos ver que o sinal da aceleração permanece o mesmo quando o sentido do movimento se inverte. Isso acontece porque a aceleração te diz apenas como a velocidade está mudando, e nesse caso ela está sempre mudando no sentido de se tornar “mais voltada para cima”.
Resposta
(a) A aceleração é sempre vertical para cima.
(b) Ver tabela.