Durante um experimento de ciência dos materiais, sobre o modulo de Young da borracha, a professora fornece à sua equipe uma tira de borracha de seção reta retangular. Ela lhes diz para primeiro medir as dimensões da seção reta e voces encontram os valores . O roteiro de laboratório determina que a tira deve ser pendurada, verticalmente, e varias massas (conhecidas) devem ser presas em sua extremidade de baixo. Sua equipe obtem os seguintes dados para o comprimento da tira como função da carga (massa) suspensa na extremidade:
![]()
- use uma planilha eletrônica, ou uma calculadora gráfica, para determinar o módulo de Young da tira de borracha nesta faixa de cagas.
- Determine a energia armazenada na tira quando a carga é
- Determine a energia armazenada na tira quando a carga é . Ela vale duas vezes o seu resultado da Parte (b)? Explique.
Passo 1
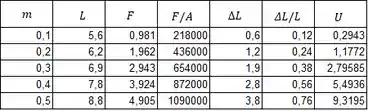
Os dados coletados são so seguintes:
![]()
Nessa questão, vamos usar a formula de Young:
Além disso,
Onde , pois temos uma massa suspensa.
Passo 2
a) Portanto, conseguimos achar as seguintes informações:
Fazendo um uma regressão linear, temos:
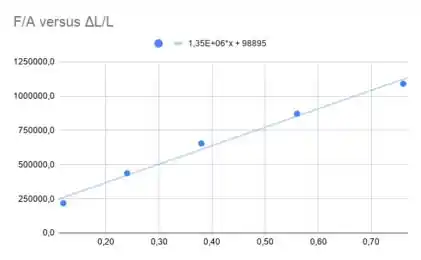
Repare que é o coeficiente angular de. Assim, podemos concluir do gráfico que:
Passo 3
b) Sabemos que
logo,
c) Agora vamos seguir a mesma ideia.
Portanto,
A energia armazena não é o dobro, pois além da massa aumentar, nosso fio também aumenta de comprimento.
Resposta
A energia armazena não é o dobro, pois além da massa aumentar, nosso fio também aumenta de comprimento.