Na figura, um bloco de é mantido em repouso através de um sistema de polias. O braço da pessoa está na vertical; o antebraço faz um ângulo com a horizontal. O antebraço e a mão têm uma massa conjunta de , com um centro de massa a uma distância à frente do ponto de contato dos ossos do antebraço com o osso do braço (úmero). Um músculo (o tríceps) puxa o antebraço verticalmente para cima com uma força cujo ponto de aplicação está a uma distância em atrás desse ponto de contato. A distância é . Quais são (a) o módulo e (b) o sentido (para cima ou para baixo) da força exercida pelo tríceps sobre o antebraço e (c) o módulo e (d) o sentido (para cima ou para baixo) da força exercida pelo úmero sobre o antebraço?
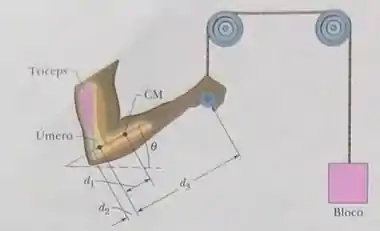
Passo 1
Como sempre, vamos desenhar um diagrama representativo das forças atuantes:
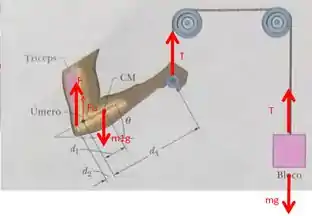
Passo 2
Agora, vamos considerar o equilíbrio de torques com relação ao ponto de contato entre o braço e o antebraço, sendo a força que o tríceps exerce entre o antebraço.
Nesse caso, , sendo a massa do bloco. Com base nisso e, “cortando” o da jogada, temos:
Passo 3
Isolando na equação acima, vem:
Passo 4
(b)Como a força encontrada acima é positiva, temos como concluir que ela está aplicada verticalmente e para cima.
Passo 5
(c)Do equilíbrio de forças na vertical, temos:
ou então
Tal que é a força exercida pelo úmero. Isolando acima, temos:
Passo 6
(d)Como a força encontrada acima está negativa, o sentido real dela é o oposto do considerado na hipótese inicial. Então podemos concluir que está aplicada na direção vertical e para baixo.
Resposta
(a)
(b)Para cima
(c)
(d)Para baixo