Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 39.1 - Ex. 9

Um elétron confinado em um poço de potencial infinito unidimensional com 250   p m de largura é transferido do primeiro estado excitado para o terceiro estado excitado. (a) Que energia deve ser fornecida ao elétron para que execute esse salto quântico? Se o elétron em seguida decai para o estado fundamental emitindo fótons, o que pode ocorrer de vária, formas, determine (b) o menor comprimento de onda. (c) o segundo menor, (d) o maior e (e) o segundo maior comprimento de onda que pode ser emitido. (f) Mostre as várias formas possíveis de decaimento em um diagrama de níveis de energia. Se um fóton com um comprimento de onda de 29,4   n m é emitido, determine (g) o maior comprimento de onda e (h) o menor comprimento de onda que pode ser emitido em seguida.

Passo 1

(a) A equação dos níveis de energia para o poço de potencial é a seguinte:

E n = n 2 h 2 8 m L 2

Se multiplicarmos e dividirmos pela velocidade da luz ao quadrado, fica (para podermos escrever as unidades em elétrons-volt):

E n = n 2 ( h c ) 2 8 m c 2 L 2

Do primeiro para o terceiro, o n vai de n = 2 até n = 4 , substituindo os dois valores, e fazendo a diferença na equação acima, a gente fica com:

∆ E = h c 2 8 m c 2 L 2 4 2 - 2 2 = 1240   e V ⋅ n m 2 8 511 × 10 3   e V 0,250   n m 2 4 2 - 2 2

∆ E = 72,2   e V

Passo 2

(b) Para calcularmos o comprimento de onda, basta usarmos a equação da velocidade da luz no vácuo para os fótons emitidos:

c = λ f

E a equação de energia quantizada:

∆ E = h f

Ficando com:

c = λ ∆ E h

λ = h c ∆ E

Como podemos ver, o menor comprimento de onda, vai ser o caso em que a diferença entre os níveis de energia é a maior, ou seja, do estado fundamental n = 1 até o estado de maior energia n = 4 :

λ 4 → 1 = 13,7   n m

Passo 3

(c) Usando o mesmo raciocínio o segundo menor vai ser:

λ 4 → 2 = 17,2   n m

Passo 4

(d) O maior comprimento vai ser do estado fundamental para o seguinte (que é o salto que tem a menor energia, já que estamos no estado fundamental):

λ 2 → 1 = 68,7   n m

Passo 5

(e) E o segundo maior comprimento, é a segunda menor energia, do estado n = 2 para o n = 3 :

λ 3 → 2 = 41,2   n m

Passo 6

(f) O diagrama com as possíveis transições será:

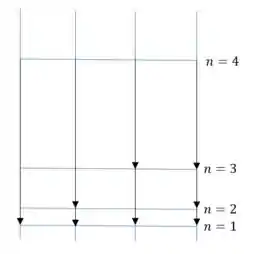
Passo 7

(g) Uma das formas é o elétron decair do nível 4 para o 3, do 3 para 1 ou do 3 para o 2 e do 2 para o 1, o maior comprimento de onda será o do nível 2 para o 1, pois será o que tem a menor energia, como já calculamos antes.

λ 2 → 1 = 68,7   n m

Passo 8

(h) Seguindo o mesmo raciocínio, o menor comprimento, será o que tem mais energia envolvida, então será do nível 3 para 1 (já que é depois do elétron já ter caído da 4 para a 3).

Esse comprimento de onda é:

λ 3 → 1 = 25,8   n m

Resposta

( a ) ∆ E = 72,2   e V

( b ) λ 4 → 1 = 13,7   n m

( c ) λ 4 → 2 = 17,2   n m

( d ) λ 2 → 1 = 68,7   n m

( e ) λ 3 → 2 = 41,2   n m

( g ) λ 2 → 1 = 68,7   n m

( h ) λ 3 → 1 = 25,8   n m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

É necessário fornecer 3,0e V de energia a um átomo para excitar um elétron do nível fundamental até o primeiro nível excitado. Considere o átomo um elétron em uma caixa e calcule a largura L da caixa.
Encontre a largura L de uma caixa de uma dimensão para a qual a energia do estado fundamental de um elétron na caixa corresponderia ao valor absoluto do nível de energia fundamental de um átomo de hid
Exercício de Livro
Um próton está em uma caixa de largura L. Qual deve ser a largura da caixa para que a energia do nível fundamental seja igual a 5,0 MeV, valor típico para a energia de ligação de partículas no interio
(a)Mostre que ψ = A c o sk x é uma solução para a equação - h / 2 π 2 2 m d 2 Ψ ( x ) d x 2 = E Ψ ( x ) se k = 2 π 2 m E / h . (b) Explique por que essa não pode ser uma função de onda aceitável para