Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 27.Exercício - Ex. 15
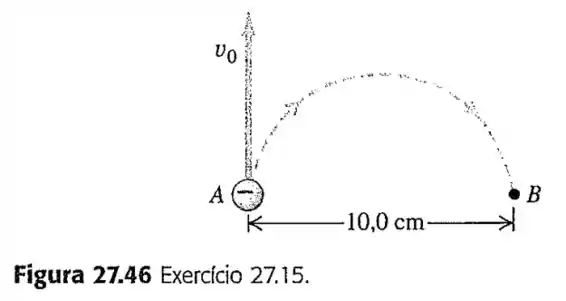
15- Um elétron no ponto da Figura possui velocidade igual a . Determine:
o módulo, a direção e o sentido do campo magnético que obriga o elétron a descrever uma órbita semicircular de até ;
o tempo necessário para que o elétron se desloque de até .
Passo 1
Se um elétron faz uma trajetória circular é por que há um campo magnético sendo aplicado perpendicularmente sobre ele de modo que a força magnética aponta para o centro de um movimento circular e portanto a força magnética será a força centrípeta desse movimento:
De modo que a intensidade do campo magnético valerá:
Onde a massa do elétron (que pode ser vista no apêndice da edição desse livro) será de:
Então:
Aí, a distância de dada é o diâmetro desse círculo e não o raio!
Passo 2
O sentido desse campo magnético é tal que a força magnética sempre aponta para dentro do círculo, de modo que temos a seguinte dinâmica no ponto mais alto da trajetória:
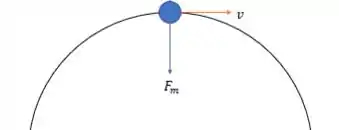
Por se tratar de uma partícula negativa, então pela regra da mão direita vemos que o campo magnético aponta de modo a entrar na página.
Passo 3
Por essa partícula percorrer metade de um círculo com a mesma velocidade então:
Pois o comprimento de um círculo é a de um semicírculo é a metade então .
Logo o tempo será de:
Tanto rápido que nem se nota.