Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 10.Exercícios e Problemas - Ex. 39
|| A mola da é comprimida em . Ela lança o bloco ao longo de uma superfície sem atrito com velocidade . As duas molas da FIGURA P10.39b são idênticas à da . Elas são comprimidas pelo mesmo total e usadas para lançar o mesmo bloco. Quanto valerá, agora, a velocidade de lançamento do bloco?
Passo 1
Um esquema é:
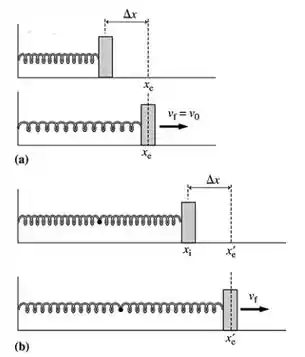
Essa questão tem um desenvolvimento muito parecida com a 38. Seremos mais rápido nessa
Passo 2
No caso
No caso , cada mola vai se comprimir por , para manter o mesmo do caso . E como são duas molas:
Fazendo igualdade das expressões que achamos:
Resposta
Exercícios de Livros Relacionados
Molas em série. Duas molas sem massa estão ligadas em série quando a ponta de uma está ligada à base da outra. a) Demonstre que a constante de força efetiva (veja Problema 6.63) de uma combinação em s
Uma força de 800N estica uma mola até uma distância de 0,200m . a) Qual é a energia potencial da mola quando ela está esticada 0,200m ? b) Qual é a energia potencial da mola quando ela está comprimida
Uma atiradeira lança verticalmente um seixo de 10g até um altura de 22,0m . a) Qual é a energia potencial elástica armazenada nas tiras de borracha da atiradeira? b) Qual seria a altura atingida por u
Uma mola ideal de massa desprezível tem 12,0 cm de comprimento quando nada está preso a ela. Ao pendurarmos um peso de 3,15 kg nessa mola, seu comprimento passa a ser 13,40 cm.Para que armazene 10,0 J
Uma mola armazena energia potencial U 0 quando está comprimida em uma distância x 0 em relação ao seu comprimento sem deformação. (a) Em termos de U 0 , quanta energia ela rmazena quando está comprimi