A bolinha de um pêndulo de comprimento L é puxada lateralmente até que o fio forme um ângulo θ 0 com a vertical e então seja liberada. No exemplo 7-5, a conservação da energia foi usada para obter a rapidez da bolinha na parte mais baixa de sua trajetória. Neste problema, você deve obter o mesmo resultado usando a segunda lei de Newton. (a) Mostre que a componente tangencial da segunda lei de Newton se escreve como d v d t = - g s e nθ , onde v é a rapidez e θ é o ângulo entre o fio e a vertical. (b) Mostre que v pode ser escrito como v = L d θ / d t . (c) Use este resultado e a regra da cadeia de derivação para obter d v d t = d v d θ v L . Combine os resultados das Partes (a) e (c) para obter v d v = - g Ls e nθd θ . (e) Integre o lado esquerdo da equação da Parte (d), de v = 0 até a rapidez final v , e o lado direito de θ = θ 0 até θ = 0 , para mostrar que o resultado é equivalente a v = 2 g h , onde h é a altura original da bolinha acima do ponto mais baixo de sua trajetória.

a ) a t a n = - g sin ⁡ θ b ) v = L d θ d t c ) d v d t = d v d θ ⋅ v L d ) - g L sin ⁡ θ d θ = v d v e ) v = 2 g h

Enunciado

Oi pessoal, tudo bem? Vamos analisar essa questão.

A situação exposta no enunciado está descrita na figura abaixo:

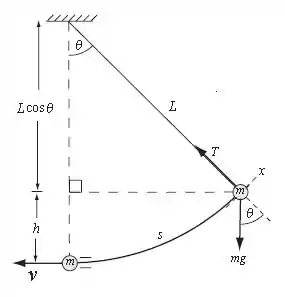
O enunciado nos diz o passo a passo que deve ser seguido, então vamos lá. Para o item (a):

Aplicando a segunda lei de Newton:

Item (b):

Relacionando o arco com o comprimento do pêndulo e o ângulo , temos:

Derivando com relação ao tempo, temos:

Item (c):

Multiplicando por e substituindo por do Passo 2, temos:

Do passo 2, sabemos que , logo:

Item (d):

Do Passo 1, sabemos que , logo:

Reorganizando, temos:

Item (e):

Agora temos que integrar nos limites disponibilizados:

Pela figura, podemos notar que , logo: