Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 7.1 - Ex. 29
29. A energia potencial de um corpo restrito ao eixo é dada por , onde está em joules e está em metros.
a) Determinea força associada a esta função de energia potencial.
b) Supondo que não haja outras forças atuando sobre o corpo, em que posições esse corpo está em equilíbrio?
c) Quais destas posições de equilíbrio são estáveis e quais são instáveis?
Passo 1
a) Sabendo que a força é definida como o negativo da derivada da função de energia potencial em relação a , ou seja, , para determinar a força associada basta então realizar o cálculo, que nada mais é do que a derivada de um polinômio de quarto grau.
Passo 2
b) O corpo está em equilíbrio, no caso, quando nenhuma força está agindo sobre ele. Ou seja as posições em que o corpo estará em equilíbrio, mais especificamente, serão aquelas em que será igual a zero.
Passo 3
c) Por último, para decidir se o equilíbrio em um ponto particular é estável ou instável, é necessário avaliar a segunda derivada da função energia potencial no ponto de interesse, no caso os pontos em que é igual a zero. Se o valor da segunda derivada resultar em um valor negativo, o equílibrio será instável, porém se o valor da segunda derivada for positivo, o equilíbrio será estável. Resta então, calcular
Deriva-se novamente, a fim de achar
Agora, basta substituir os três pontos de interesse na expressão da segunda derivada e verificar se o valor encontrado é positivo ou negativo:
Para :
Para :
Para :
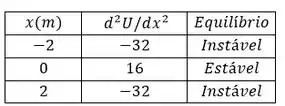
A seguinte tabela abaixo mostra o valor de , da segunda derivada e do tipo de equílibrio:
Resposta