Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 10.Exercícios e Problemas - Ex. 37
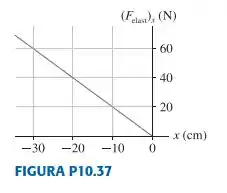
|| Uma pedra de é colocada em um estilingue e a tira de borracha é esticada. A força resultante da tira sobre a pedra é representada no gráfico da .
A tira de borracha foi esticada para a direita ou para a esquerda? Como você pode descobrir isso?
Esta tira de borracha satisfaz à lei de ? Explique.
Quanto vale a constante elástica da tira de borracha?
A tira de borracha é esticada em e, depois é liberada. Qual será o módulo da velocidade de arremesso da pedra?
Passo 1
Um esquema é:
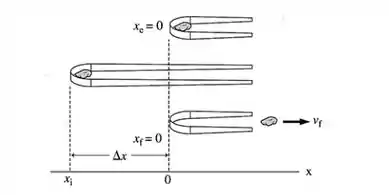
Passo 2
A tira de borracha foi esticada para a direita ou para a esquerda? Como você pode descobrir isso?
Esquerda.
A tira de borracha tem que ser esticado para a esquerda, pois segundo o gráfico, uma força positiva na pedra () é devida a um deslocamento negativo.
Ou seja,
em que é o deslocamento da pedra.
Passo 3
Esta tira de borracha satisfaz à lei de ? Explique.
Sim!
A condição gráfica para se ter lei de Hooke é ser linear com ângulo negativo. Exatamente como o gráfico do problema.Lembre-se:
Passo 4
Quanto vale a constante elástica da tira de borracha?
Escolhendo qualquer ponto do gráfico para relacionar com e , aplicando a lei de Hooke, encontramos , por exemplo:
Passo 5
A tira de borracha é esticada eme, depois é liberada. Qual será o módulo da velocidade de arremesso da pedra?
Mas uma vez podemos usar o principio de conservação da energia mecânica, mas dessa vez em vez do tradicional (energia potencial gravitacional), vãos usar a (energia potencial elástica.)
Então teremos:
Já temos ,
Resposta
Esquerda.
A tira de borracha tem que ser esticado para a esquerda, pois segundo o gráfico, uma força positiva na pedra () é devida a um deslocamento negativo.
Sim!
A condição gráfica para se ter lei de Hooke é ser linear com ângulo negativo. Exatamente como o gráfico do problema