Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 15.Problemas - Ex. 62

A Equação (15.7) para uma onda senoidal pode ser generalizada ainda mais incluindo o ângulo de fase ϕ , onde 0 ≤ ϕ ≤ 2 π (em radianos). Então, a função de onda y ( x , t ) se escreve na forma y x , t = A cos ⁡ ( k x - ω t + ϕ ) . a) Faça um desenho da onda em função de x no instante t = 0 para ϕ = 0 , ϕ = π / 4 , ϕ = π / 2 , ϕ = 3 π / 4 e ϕ = 3 π / 2 .b) Ache a velocidade transversal v y = ∂ y / ∂ t .c) Para t = 0 , uma partícula dobre a corda em x = 0 possui deslocamento y = A / 2 . Essa informação é suficiente para determinar o valor de ϕ ? Se, além disso, você for informado que uma partícula sobre a corda em x = 0 se desloca em y = 0 no instante t = 0 , qual é o valor de ϕ ?d) Explique de modo geral o que você deve conhecer do comportamento da onda em um dado instante para determinar o valor de ϕ .

Passo 1

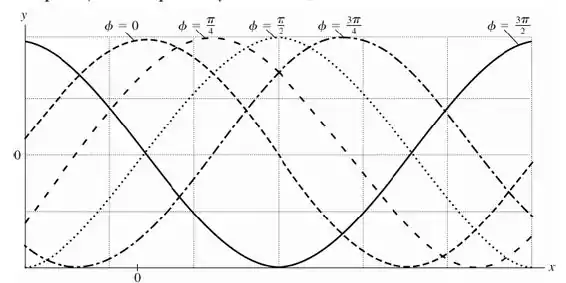
O ângulo de fase determina o valor de y para x = 0 , t = 0 , mas não afeta a forma do gráfico de y   ( x ,   t ) versus x ou t .

∂ cos ⁡ ( k x - ω t + ϕ ) ∂ t = - ω   s e n   k x - ω t + ϕ .

Passo 2

  1. Os gráficos de cada φ são esboçados a seguir:

    2. Passo 3

  2. Para encontrarmos a velocidade transversal v y = ∂ y / ∂ t :

    3. ∂ y ∂ t = - ω A   s e n   ( k x - ω t + ϕ )

    Passo 4

  3. Não.

    4. ϕ = π 4 ou ϕ = 3 π 4

    ambos dariam A / 2 .

    Se se sabe que a partícula está se movendo para baixo, o resultado da parte (b) mostra que

    cos ⁡ ϕ < 0 ,

    e então

    ϕ = 3 π / 4 .

    Passo 5

  4. Para identificar ϕ exclusivamente, o quadrante em que ϕ reside deve ser conhecido. Em termos físicos, os sinais da posição e da velocidade, e a magnitude de qualquer uma, são necessários para determinar ϕ (dentro de múltiplos aditivos de 2 π ).

A fase   ϕ = 0 corresponde a y = A em x = 0 ,   t = 0 .

Resposta

  2. - ω A   s e n   ( k x - ω t + ϕ )
  3. Não
  4. Explicado no passo 5.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

a)Mostre que a Equação (15.25) pode ser estrita do seguinte modo: P m é d = 1 2 F k ω A 2 é , onde k é o numero de onda da onda.b) Se a tensão F na corda quadriplicar enquanto a amplitude A permanecer
Um pulso ondulatório triangular em uma corda esticada propaga-se no sentido +x com velocidade v . A tensão na corda é F , e a densidade linear da corda é μ . Em t = 0 , a forma do pulso é dada por y x
Uma corda esticada está sobre o eixo O x . A corda é deslocada nos sentidos y e z , de modo que o deslocamento transversal da corda seja dado por y x , t = A cos ⁡ ( k x - ω t ) z x , t = A sen ⁡ ( k
Uma barra uniforme de 165N é sustentada horizontalmente por dois fios idênticos, A e B (Figura 16.43). Um pequeno cubo de chumbo de 185N é colocado a 3 / 4 do caminho entre A e B . Os fios medem cada