Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 15.Problemas - Ex. 64

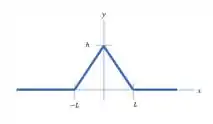
Um pulso ondulatório triangular em uma corda esticada propaga-se no sentido +x com velocidade v . A tensão na corda é F , e a densidade linear da corda é μ . Em t = 0 , a forma do pulso é dada por

y x , 0 = 0                                                                                               s e   x < - L h ( L + x ) / L                                               p a r a   - L < x < 0   h ( L - x ) / L                                           p a r a   0 < x < L 0                                                                                     p a r a   x > L          

a)Desenhe o pulso em t = 0 ; b) Determine a função de onda y x , t em todos os tempos t . c) Ache a potencia instantânea na onda. Mostre que a potencia é igual a zero a não ser para - L < x - v t ) < L e que nesse intervalo a potencia é constante. Calcule o valor dessa potencia constante.

Passo 1

A onda se move na direção x com a velocidade v , portanto, para obter y   ( x ,   t ) , substitua x por x - v t na expressão para y   ( x ,   0 ) .

P   ( x ,   t ) é dado pela equação:

P x , t = F y x , t v - y   x , t = - F ∂ y x , t ∂ x   ∂ y ( x , t ) ∂ t

Passo 2

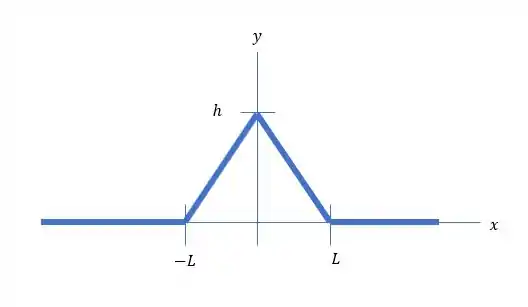
  1. O pulso da onda é esboçado na Figura a seguir:

    2. Passo 3

  2. E a função de onda y x , t em todos os tempos t é:

    3. y x , t = 0                                                                 p a r a   x - v t < - L h L + x - v t L                                   p a r a - L < x - v t < 0 h L - x + v t L                             p a r a       0 < x - v t < L 0                                                           p a r a     x - v t > L

    Passo 4

  3. Da equação P x , t = F y x , t v - y   x , t = - F ∂ y x , t ∂ x   ∂ y x , t ∂ t :

P x , t = - F   ∂ y x , t ∂ x   ∂ y x , t ∂ t = - F 0 0 = 0                                                         p a r a   x - v t < L - F h L - h v L = F v h L 2                       p a r a - L x - v t < 0 - F - h L h v L = F v h L 2                     p a r a   0 < x - v t ) < L - F 0 0 = 0                                                   p a r a   x - v t > L

Assim, a potência instantânea é zero, exceto para - L < x - v t < L , onde tem o valor constante F v h L 2 .

Para este pulso, a velocidade transversal v y é constante em magnitude e tem sinal oposto em ambos os lados do pico do pulso. 

Resposta

  2. y x , t = 0                                                                 p a r a   x - v t < - L h L + x - v t L                                   p a r a - L < x - v t < 0 h L - x + v t L                             p a r a       0 < x - v t < L 0                                                           p a r a     x - v t > L
  3. P x , t = - F   ∂ y x , t ∂ x   ∂ y x , t ∂ t = - F 0 0 = 0                                                         p a r a   x - v t < L - F h L - h v L = F v h L 2                       p a r a - L x - v t < 0 - F - h L h v L = F v h L 2                     p a r a   0 < x - v t ) < L - F 0 0 = 0                                                   p a r a   x - v t > L
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um fio de 5,0 m e 0,732 kg é usado para sustentar dois postes uniformes de 235 N de igual comprimento (Figura 15.37). Suponha que o fio esteja na horizontal e que a velocidade do som seja 344 m/s. Um
A forma de uma onda em uma corda em um instante especifico e mostrada na Fifura 14.38. A onda está se deslocando para a direita, no sentido +x. a) Determine o sentido da velocidade transversal dos sei
a)Faça um desenho de y ( x , t ) dado pela Equação (15.7) em função de x no instante t (digamos para t=0). Sobre os mesmos eixos, fala um desenho d potencia instantânea P ( x , t ) dado pela Equação (
Uma sucessão contínua de pulsos ondulatórios senoidais é produzida em uma extremidade de uma corda bastante longa e se propaga por toda a extensão da corda. A onda possui uma frequência de 40,0 Hz amp
Uma onda transversal senoidal com amplitude igual a 2,5 mm e comprimento de onda igual a 1,8 m propaga-se com velocidade de 36,0 m/s da esquerda para a direita ao longo de uma corda sem perturbação. N