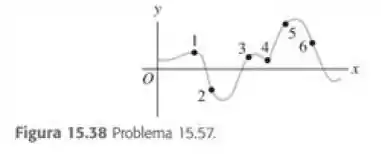
A forma de uma onda em uma corda em um instante especifico e mostrada na Fifura 14.38. A onda está se deslocando para a direita, no sentido +x. a) Determine o sentido da velocidade transversal dos seis pontos assinalados sobre a cruva. Quando a velocidade for nula, mencione esse fato. Explique seu raciocínio. b) Determine o sentido da aceleração transversal dos sis pontos assinalados sobre a curva. Explique seu raciocínio. c) Como suas respostas deveriam ser alteradas se a onda está se deslocando para a esquerda, no sentido -x?

1. E (b):

Ponto (1): A curva parece ser horizontal e . Conforme a onda se move, o ponto será

começa a se mover para baixo e .

Ponto (2): À medida que a onda se move na direção , a partícula se move para cima, então . A parte da curva à esquerda do ponto é mais íngreme, então .

Ponto (3): O ponto está se movendo para baixo e aumentará sua velocidade à medida que a onda se mover; , .

Ponto (4): A curva parece ser horizontal e . Como a onda se move, o ponto se afasta do e .

Ponto (5): O ponto está se movendo para baixo e aumentará sua velocidade à medida que a onda se mover; , .

Ponto (6): A partícula está se movendo para cima, mas a curva que representa que a onda parece não ter curvatura, então e.

(c) As acelerações relacionadas às curvaturas não serão alteradas. As velocidades transversais mudarão de sinal.