Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 17.Problemas - Ex. 89
- A equação (17.12) fornece a tensão necessária para manter constante o comprimento da barra à medida que a temperatura varia. Mostre que, se o comprimentpo pudesse variar de quando sua temperatura varia de , a tensão seria dada por
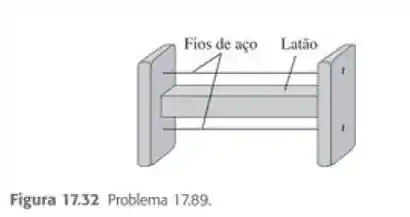
onde F é a tensão na barra, é o comprimento original da barra, A é a área de seção reta, é o coeficiente de dilatação linear e Y é o modulo de Young. b) Uma pesada barra de latão possui duas projeções ligadas em suas extremidades, como mostra a Figura 17.32. Dois fios finos de aço amarrados entre as projeções estão apenas levemente esticados (sem nenhuma tensão) quando o sistema está a . Qual é a tensão de dilatação nos fios de aço quando a temperatura do sistema se eleva até ? Faça as hipóteses simplificadoras que julgar necessárias, porém enuncie e explique o que elas significam.
Passo 1
A mudança de comprimento devido ao aquecimento é:
e isso não precisa ser igual a .
A mudança de comprimento devido à tensão é:
Sendo que .
Sabemos que:
Passo 2
- A mudança no comprimento é devido à tensão e aquecimento.
- A barra de latão é dada como "pesada" e os fios são "finos", portanto, pode-se supor que a tensão na barra devido aos fios finos não afeta a quantidade pela qual a barra se expande devido ao aumento da temperatura. Este significa que não é zero, mas é a quantidade de latão que o latão expande e, portanto,
Resolvendo para :
Passo 3
O comprimento da barra de latão aumenta mais que o comprimento dos fios de aço. Os fios permanecem tensos e estão sob tensão quando a temperatura do sistema é elevada acima de .