Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Problemas - Ex. 73

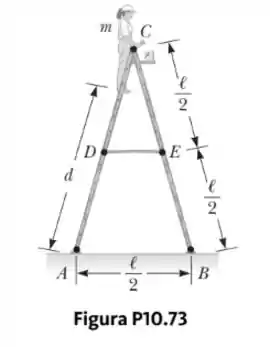
Uma escada portátil de peso desprezível é construída como mostrado na Figura P10.73, com A C   =   B C   =   l   =   4,00   m . Um pintor de massa m   =   70,0   k g sobe na escada d   =   3,00   m do chão. Considerando o piso sem atrito, encontre

  1. a tensão na barra horizontal D E que conecta as duas metades da escada,
  2. as forças normais em A e B , e
  3. as componentes da força de reação na dobradiça única C que a metade esquerda da escada exerce sobre a metade direita.

Sugestão: Trate a escada como um corpo único, mas também trate cada metade da escada separadamente.

Passo 1

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

Pela geometria da escada, observe que:

cos ⁡ θ = 1 4 → θ = 75.5 ∘

A seguir, usamos as variáveis ​​ m = 70.0 k g ,   comprimento   A C = B C = l = 4.00 m ,   e  d = 3.00 m ;

Considere o torque sobre o ponto A (no lado esquerdo inferior da escada) de forças externas em toda a escada. Os torques sobre A vêm do peso da pessoa e da força normal n B .

∑ τ A = - m g d c o s ⁡ 75.5 ∘ + n B l 2 = 0 → n B = 2 l m g d c o s ⁡ 75.5 ∘ = 2 l m g d 1 4 → n B = m g d 2 l

Considere o líquido sobre o ponto B (no lado inferior direito da escada) de forças externas em toda a escada. Os torques sobre B vêm do peso da pessoa e da força normal n A :

∑ τ B = - n A l 2 + m g l 2 - dcos ⁡ 75.5 ∘ = 0 → n A l 2 = m g l 2 - dcos ⁡ 75.5 ∘

n A = 2 l m g l 2 - dcos ⁡ 75.5 ∘ n A = m g 1 - d 2 l

Considere o torque de forças externas sobre o ponto C no topo direito da escada:

∑ τ C = - T l 2 s i n ⁡ 75.5 ∘ + n B l 4 = 0 → T = n B 1 2 sin ⁡ 75.5 ∘ = m g d 2 l 1 2 sin ⁡ 75.5 ∘ → T = m g d 4 l sin ⁡ 75.5 ∘

Agora encontramos os componentes da força de reação que a metade esquerda da escada exerce na metade direita. Considere as forças agindo sobre a metade direita da escada:

∑ F x = R x - T = 0 → R x = T ,   à   d i r e i t a ∑ F y = R y + n B = 0 → R y = - n B → R y = n B ,   p a r a   b a i x o  

Então, encontramos:

Passo 2

Letra a:

T = m g d 4 l sin ⁡ 75.5 ∘ = 70.0 k g 9.80 m s 2 3.00 m 4 4.00 m 1 4

T = 133 N

Passo 3

Letra b:

n A = m g 1 - d 2 l n A = ( 70.0 k g ) 9.80 m s 2 1 - 2 3.00 m 1 4 4.00 m → n A = 429 N

n B = m g d 2 l = 70.0 k g 9.80 m s 2 3.00 m 2 4.00 m → n B = 257 N

Passo 4

Letra c:

R x = T → R x = 133 N ,   para a direita

R y = - n b → R y = - 257 N → R y = 257 N ,   para baixo

Resposta

  1. T = 133 N
  2. n A = 429 N   e   n B = 257 N
  3. R x = T → R x = 133 N ,  para a direita e R y = - n b → R y = - 257 N → R y = 257 N ,  para baixo
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um equilibrista procura manter sempre seu centro de massa verticalmente acima do arame (ou corda). Para isso, carrega muitas vezes uma vara comprida. Quando se inclina, digamos, para a direita (desloc
N a Fig. 10-52, uma roda com 0,20m de raio é montada em um eixo horizontal sem atrito. Uma corda de massa desprezível é enrolada na roda e presa a uma caixa de 2,0k g que escorrega sobre uma superfíci
Na Fig. 10-47, dois blocos de 6,20k g estão ligados por uma corda de massa desprezível que passa por uma polia de 2,40c m de raio e momento de inércia 7,40 * 10 - 4 k g · m 2 . A corda não escorrega n
Nas duas extremidades de uma fina barra de aço com 1,20m de comprimento e 6,40k g de massa existem pequenas bolas de massa 1,06k g . A barra pode girar em um plano horizontal em tomo de um eixo vertic
Uma casca esférica fina tem um raio de 1,90m . Um torque aplicado de 960N · m produz uma aceleração angular de 6,20r a d / s 2 em relação a um eixo que passa pelo centro da casca. Quais são (a) o mome