Um filete de água escorre verticalmente de uma torneira de raio , com o escoamento estacionário de vazão . Ache a forma do jato de água que cai, determinando o raio da secção transversal em função da altura de queda.
Passo 1
Vamos começar fazendo um desenho da situação:
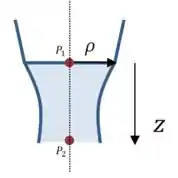
Podemos escrever a equação de Bernoulli entre os pontos e :
Os dois pontos estão sobre a superfície, então :
E como a origem do sistema está na altura de , temos e :
Passo 2
E agora vamos aplicar a equação da continuidade nesses dois pontos.
Podemos chamar de o raio da torneira no ponto , e de o raio no ponto :
Elevando os dois lados ao quadrado:
E substituindo na equação de Bernoulli:
E nosso objetivo é achar em função de :
Passo 3
Para simplificar, vamos chamar essa velocidade de :
E ela pode ser calculada a partir do raio da torneira e da vazão volumétrica :
Agora sim, nossa resposta só depende de variáveis que foram dadas no enunciado.
Resposta
O raio é dado por , com .