Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 72
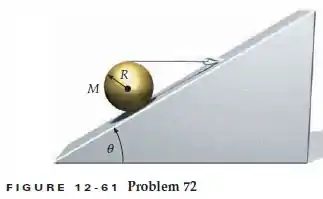
Uma esfera homogênea, de raio R e massa M, é mantida em repouso, por um cordão horizontal, sobre um plano inclinado de um ângulo , como mostrado na Figura 12-61. Seja , e
- Qual é a tração no cordão?
- Qual é a força normal exercida sobre a esfera pelo plano inclinado?
- Qual é a força de atrito atuando sobre a esfera?
Passo 1
Bom, pelo que o problema nos disse a bola está em equilíbrio no plano inclinado. Então, as duas condições são satisfeitas:
Vamos ilustrar as forças que atuantes sobre a bola:
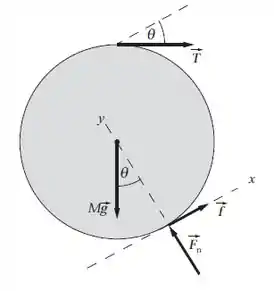
No centro de gravidade, ou seja, no ponto central da bola de aço, temos a força gravitacional sendo aplicada para baixo formando um ângulo com o eixo y (chegamos nesse resultado por causa da trigonometria, ok?!). Dada por:
Como nós temos duas superfícies em contato, existe a força normal , perpendicular ao plano inclinado, e a força de atrito. O cabo suportando a bola também gera uma força de tração (T), formando um ângulo com o eixo x.
Muito bem, já sabemos as forças que atuam no corpo agora precisamos trabalhar com as nossas condições.
Passo 2
Vamos começar usando o torque! Que é calculado como:
Onde r é a distância entre a força e o eixo de rotação. A escolha do eixo será muito importante, e aqui vamos escolher o ponto central da bola, passando sobre a força normal. Quando fazemos isso a distância para a força normal e peso se igualam a 0. A distância até as demais forças é
Colocando no torque:
Então galera, usando as segunda condição do equilíbrio já conseguimos achar a uma relação entre as forças, mas não é suficiente para resolvermos o problema.
Passo 3
Como ainda não temos informação suficiente, vamos precisar de mais uma relação, podemos usar para isso a primeira condição.
Se , então .
Na direção x, nós temos três forças atuando: a força de atrito (), a componente x da força peso () e da tração ():
Lembrando da igualdade do passo 1:
Isolando T:
Já sabemos que:
Se
Passo 4
Já sabemos a resposta para as letras a e c, agora falta acharmos a força normal. Vamos usar a única informação que não usamos,
Na direção y, nós temos três forças atuando: a força normal, a componente y da força peso () e da tração ():
Substituímos os dados:
Resposta
- ;