Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 7.Problemas - Ex. 1
Uma esfera oca de alumínio tem um raio interno de e raio externo de a . O coeficiente de dilatação linear do alumínio é . De quantos varia o volume da cavidade interna quando a temperatura sobre para ? O volume da cavidade aumenta ou diminui?
Passo 1
Vamos fazer um desenho em “corte” da esfera oca antes e depois da expansão:
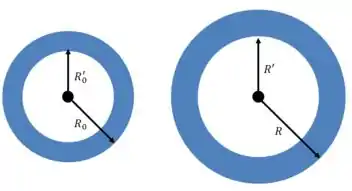
Quando um corpo se expande pelo efeito da temperatura, todas as suas dimensões lineares crescem igualmente. Isso inclui os “buracos” no seu interior.
É como se você desse um “zoom” no objeto, as suas proporções não devem mudar.
Então podemos tratar a dilatação do raio interno da mesma forma que trataríamos uma esfera inteira.
Passo 2
A fórmula para a dilatação volumétrica é:
E o coeficiente de dilatação volumétrica é o triplo do coeficiente de dilatação linear que foi dado no enunciado:
Como , temos:
Passo 3
Só para garantir que não ficou nenhuma dúvida: por que a esfera não se expande nas duas direções? Por que a dilatação não faz a cavidade fechar?
Uma forma de entender isso é pensar que a expansão quer preservar a forma do objeto. Essa forma inclui a proporção entre o raio interno e o externo.
Para mudar a forma, você teria que aumentar a “tensão” interna do objeto, e isso consome energia. Em outras palavras, o caminho de menor energia é preservar o formato!
Por isso, o volume da cavidade aumenta junto com o volume total da esfera.
Resposta
O volume da cavidade aumenta em .