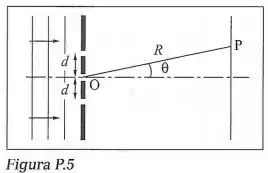
Uma onda sonora plana harmônica de comprimento de onda incide perpendicularmente sobre um anteparo opaco com três fendas igualmente espaçadas, de espaçamento . Para pontos de observação situados a distâncias , determine as direções de observação (Fig. P.5) em que aparecem mínimos de interferência, generalizando a (6.8.11) de duas para três fendas. Qual é a intensidade dos mínimos?
Passo 1
Bom, vamos chamar a fenda superior de e a fenda inferior de . Na seção 6.8 do livro, foi deduzido a expressão de interferência para fendas duplas. Para isso, foi considerado a função de onda proveniente de cada fenda se propagando até chegar no ponto e daí, pelo princípio de superposição, a função de onda resultante era a soma das funções de onda proveniente de cada fenda. Assim, nesse nosso caso, teremos
Vamos considerar o caminho que a onda que sai de cada fenda percorre:

*Essa figura foi retirada do livro e adaptada.
Usando notação real, teríamos
No caso das duas fendas já foi bastante trabalhoso “brincar” com os cossenos. No caso de três fendas seria muito mais complicado. Por isso, vamos usar a notação complexa! A ideia é muito simples, mas primeiro você deve conhecer a fórmula de Euler:
Portanto,
O que nós vamos é o seguinte: vamos usar a função de onda complexa!
Como isso, a função de onda resultante será
Passo 2
Assim, temos que
Note que todos os termos têm , de modo que podemos puxar ele em evidência:
Agora vamos fazer uma daquelas aproximações que os físicos sempre fazem e que os alunos não gostam num primeiro momento. É evidente que . Todavia, como a distância entre as fendas é pequena, , e são bem próximos. Note que eles aparecem em dois lugares: no denominador e na exponencial complexa. No denominador eles tem um papel de atenuação apenas, enquanto na exponencial eles determinam as fases das oscilações, que é um efeito muito mais significativo numericamente do que a atenuação. Desta forma, por simplicidade, adotamos no denominador porém mantemos a distinção deles na exponencial:
Eu sei que essas aproximações parecem bruxarias, mas elas nos levam a resultados muito precisos e isso foi feito na dedução da fenda dupla feita no livro. Se você quiser conferir lá, dá uma olhada entre as equações 6.8.3 e 6.8.4.
Passo 3
Bom, agora vamos ver a parte onde aparece a interferência! Para isso, considere a figura:
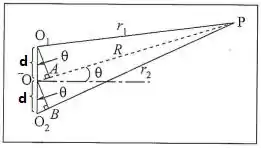
*Essa figura foi retirada e adaptada do livro.
Para , temos que
Assim,
Portanto,
Vamos chamar e puxar em evidência:
Além disso, vou puxar para fora no termo em colchetes:
Assim,
Passo 4
Agora, para achar a intensidade, fazemos
Mas cuidado, esse módulo aqui é o módulo complexo, não basta elevar ao quadrado:
Lembre-se que é o complexo conjugado de . Se , . Assim, basta pegar todos os ligares onde aparece e trocar por .
Note que
Assim,
O termo que realmente importa para a interferência é
Passo 5
O enunciado deu como sugestão que
Assim,
A seguir faço um plot dessa função de :

A intensidade se anula quando
se anula mas
não se anula! Quando ambos se anula, temos uma indeterminação do tipo que converge!
Assim, os mínimos de intensidade ocorrem para
Isso pois quando é inteiro, temos que
Caso não seja inteiro, . Assim, temos que
Mas lembre-se que
Assim,
Sabemos também que
Portanto, os ângulos em que a intensidade é nula (mínima), são dados pela relação