Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 76

Uma esfera sólida não condutora tem diâmetro igual a 1,20   m , tem seu centro no eixo x em x = 4,00   m e tem uma densidade volumétrica uniforme de carga de + 5,00   μ C / m 3 . Uma fina casca esférica não condutora é concêntrica à esfera, tem diâmetro de 2,40   m e densidade superficial uniforme de carga de - 1,50   μ C / m 2 . Calcule o módulo, a direção e o sentido do campo elétrico em (a) x = 4,50   m , y = 0 , (b) x = 4,00   m , y = 1,10   m e (c) x = 2,00   m e y = 3,00   m .

Passo 1

A figura abaixo ilustra o que o enunciado disse.

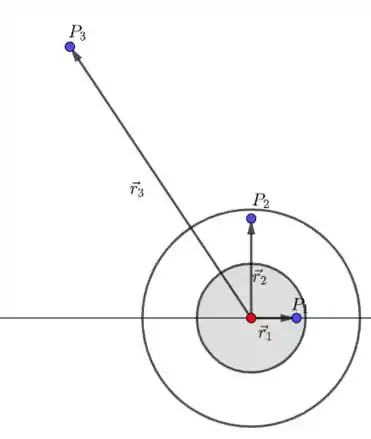
Passo 2

  1. Aplicando a lei de Gauss, temos

    2. ∫ E 1   d A = q i n t ε 0

    Porém, temos que

    q = ρ ⋅ 4 3 π r 1 3

    De forma eu

    E 4 π r 1 2 = 4 3 ρ π r 1 3 ε 0 ⟹ E = ρ r 1 3 ε 0

    Ou, em termos vetoriais,

    E → = ρ 3 ε 0 r → 1

    Notemos que

    r → 1 = 0,50   m i ^

    Assim,

    E → = 5,00 × 10 - 6 3 8,85 × 10 - 12 0,50 i ^ = 94,2   k N / C i ^

    Assim, o módulo vale

    E → = 94,2   k N / C

    Passo 3

  2. Da mesma forma, temos que

    3. ∮ E   d A = q i n t ε 0 E 4 π r 2 2 = ρ ⋅ 4 3 π R 1 3 ε 0 E = ρ R 1 3 3 ε 0 r 2 2

    Ou, em termos vetoriais,

    E → = ρ R 1 3 3 ε 0 r 2 2 r ^ 2 = ρ R 1 3 3 ε 0 r 2 3 r → 2

    notemos que

    r → 2 = 1,10   m j ^

    Assim, segue que

    E → = 5,00 × 10 - 6 0,60 3 3 8,85 × 10 - 12 1,10 3 1,10 j ^ = 33,6   k N / C j ^

    O módulo será:

    E → = 33,6   k N / C

    Passo 4

  3. Temos

∮ E ⋅ d A = Q i n t ε 0

onde

Q i n t = q 1 + q 2 = 4 3 π ρ R 1 3 + 4 π σ R 2 2 Q i n t = 4 3 π 5,00 × 10 - 6 0,60 3 + 4 π - 1,50 × 10 - 6 1,20 2 Q i n t = - 2,26 × 10 - 5   C

Ou seja,

E 4 π r 3 2 = Q i n t ε 0 ⟹ E = Q i n t 4 π ε 0 r 3 2 E = k Q i n t r 3 2

Em termos vetoriais, temos

E → = k Q i n t r 3 3 r → 3

onde

r → 3 = - 2,00   m i ^ + 3,00   m j ^

Dessa forma, segue que

E → = 9 × 10 9 - 2,26 × 10 - 5 - 2,00 2 + 3,00 2 3 2 - 2,00 i ^ + 3,00 j ^ E → = 8,67   k N / C i ^ + - 13,0   k N / C j ^

O módulo será:

E → = 8,67 2 + - 13,0 2 = 15,6   k N / C

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se o fluxo elétrico através de uma superfície fechada por igual o zero, o campo elétrico deve ser zero em todos os pontos desta superfície? Se a reposta for não, dê um exemplo específico. A partir da
Explique por que a intensidade do campo elétrico aumenta linearmente com r no lugar de decrescer com inverso de r 2 entre o centro e a superfície de uma esfera sólida carregada uniformemente.
Verdadeiro ou falso:O campo elétrico devido a uma fina casca esférica oca, uniformemente carregada, é zero em todos os pontos no interior da casca. Em equilíbrio eletrostático, o campo elétrico em qua
Verdadeiro ou falso: A lei de Gauss vale apenas para distribuições simétricas de carga. O resultado que E = 0 para todos os pontos no interior do material de um condutor em condições eletrostáticas po
Medidas cuidadosas do campo elétrico na superfície de uma caixa preta indicam que o fluxo elétrico resultante saindo da superfície da caixa é 6,0k N ⋅ m 2 / C . (a) Qual é a carga resultante dentro da