Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 9.10 - Ex. 62

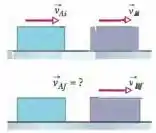
Na Fig. 9-64, o bloco A (com uma massa de 1,6   k g ) desliza em direção ao bloco B (com uma massa de 2,4   k g ) ao longo de uma superfície sem atrito. Os sentidos de três velocidades antes ( i ) e depois ( f ) da colisão estão indicados; as velocidades escalares correspondentes são V A i =   5,5   m / s , v B i   =   2,5   m / s e v B f   =   4,9   m / s . Determine (a) o módulo e (b) o sentido (para a esquerda ou para a direita) da velocidade v → A f · (c) A colisão é elástica?

Passo 1

Então galera , seja m A a massa do bloco da esquerda, seja v A i     a velocidade inicial desse bloco e seja v A f   a velocidade final desse bloco. Seja m B a massa do bloco da direita, seja v B i   a velocidade inicial desse bloco e seja v B f   a velocidade final desse bloco. Como o momento do sistema de dois blocos é conservado, temos que :

m A v A i   +   m B v B i   =   m A v A f   +   m B v B f

v A f = m A v A i + m B v B i - m B v B f m A = 1,6 k g 5,5 m s + 2,4 k g 2,5 m s - 2,4 k g 4,9 m s 1,6   k g

v A f = 1,9 m / s

Passo 2

Bom pessoal , reparem que o bloco continua a se mover para a direita após a colisão uma vez que ambos os blocos estavam indo nessa mesma direção antes da colisão.

Passo 3

Agora , para verificarmos se a colisão é elástica, comparamos a energia cinética total antes da colisão com a energia cinética total após a colisão. A energia cinética total antes da colisão é

K i = m 1 v 1 i 2 2 + m 2 v 2 i 2 2 = 1 2 1,6 5,5 2 + 1 2 2,4 2,5 2 = 31,7 J

A energia cinética total após a colisão é

K f = m 1 v 1 f 2 2 + m 2 v 2 f 2 2 = 1 2 1,6 1,9 2 + 1 2 2,4 4,9 2 = 31,7 J

Como Ki = Kf, a colisão é elástica.

Resposta

Respectivamente :

v A f = 1,9 m s

O bloco continua a se mover para a direita após a colisão.

A colisão é elástica.

Tranquilo galera? Bora resolver mais questões então

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Amplificador de velocidade. Na Fig. 9-75, o bloco 1, de massa m 1 , desliza ao longo de um eixo x em um piso sem atrito, com uma velocidade v 1 i =4,00r n / s , até sofrer uma colisão elástica unidime
Amplificador de velocidade. Na Fig. 9-75, o bloco 1, de massa m 1 , desliza ao longo de um eixo x em um piso sem atrito, com uma velocidade v 1 i=4,00m / s , até sofrer uma colisão elástica unidimensi
As três bolas vistas de cima na Fig. 9-76 são iguais. As bolas 2 e 3 estão se tocando e alinhadas perpendicularmente à trajetória da bola 1. A velocidade da bola 1 tem módulo v 0=10 m / s e está dirig
No arranjo da Fig. 9-21, a bola de sinuca 1, que se move a 2,2m / s , sofre uma colisão oblíqua com a bola de sinuca 2, que está inicialmente em repouso. Após a colisão, a bola 2 se move com uma veloc
Um objeto de 3,0k g , que se move com uma velocidade escalar de 8,0m / s no sentido positivo de um eixox , sofre uma colisão elástica unidimensional com um objeto de massa M inicialmente em repouso. A