Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.2 - Ex. 13

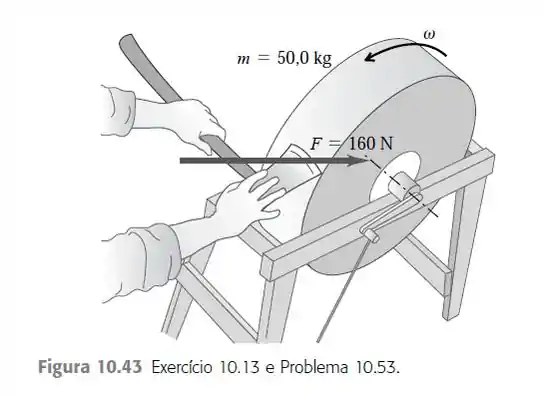
Um esmeril em forma de disco sólido com diâmetro de 0,520   m e massa de 50,0   k g   gira a 850   r e v / m i n . Você pressiona um machado contra sua periferia com uma força normal de   160   N (Figura 10.43), e o esmeril atinge o repouso em   7,50   s . Ache o coeficiente de atrito entre o machado e o esmeril. Despreze o atrito nos mancais.

Passo 1

Eaee, belezinha?? Bom... o enunciado nos diz que um esmeril em forma de disco sólido com diâmetro de 0,520   m e massa de 50,0   k g   gira a 850   r e v / m i n .

Queremos encontrar o coeficiente de atrito entre o esmeril e um machado quando alguém pressiona um machado contra sua periferia com uma força normal de   160   N e o esmeril atinge o repouso em   7,50   s .

Para isso, vamos utilizar das informações cinemáticas para resolver a aceleração angular da pedra de amolar (ou esmeril como o problema preferiu chamar).

Suponhamos que o o rebolo está girando no sentido anti-horário e seja esse o sentido positivo de rotação.

Em seguida, aplique a forma análoga da segunda lei de Newton, ∑ τ = I α , para a rotação de um corpo rígido e calcular a força de atrito, usando f a t k = μ k N para calcular μ k .

Com isso, vamos chegar na relação,

∑ τ = I α = - f k R = - μ k N R

Agora vamos aplicar! 😉

Passo 2

O enunciado forneceu,

ω 0 = 850 r e v m i n ⋅ 2 π r a d 1 r e v ⋅ 1 m i n 60 s = 89 r a d s t = 7,50 s ω = 0

E queremos encontrar a aceleração, α , através da equação:

ω = ω 0 + α t

⇒ α = 0 - 89 r a d / s 7,50 s = - 11,9 r a d / s 2

Passo 3

Esboçando o diagrama de corpo livre da pedra de amolar, temos:

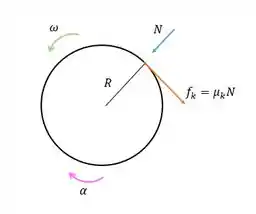
A força normal possui um braço de momento zero para rotação em torno de um eixo no centro da pedra de amolar e, portanto, zero torque.

O único torque na pedra de amolar é aquele devido à força de atrito f k exercida pelo machado; por esta força a o momento do braço é l = R e o torque é negativo.

Então, aplicando,

∑ τ = I α = - f k R = - μ k N R

E sabemos que a inércia do disco sólido, no eixo através do centro, é dada por

I = 1 2 M R 2

Passo 4

Dessa forma, substituindo I e τ , temos:

- μ k N R = 1 2 M R 2 α

⇒ μ k = - M R α 2 N = - 50 k g ⋅ 0,260 m ⋅ ( - 11,9 r a s / s 2 ) 2 ⋅ 160 N = 0,483

O torque de fricção é no sentido horário e diminui a rotação no sentido anti-horário da pedra de amolar.

Resposta

μ k = 0,483

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cordão é amarrado ao redor de um disco uniforme de raio R e massa M . O disco é solto do repouso com o cordão vertical e sua ponta de cima amarrada a uma barra fixa (Fig. P10.78). Mostre que a tens
Uma barra uniforme longa de comprimento L e massa M é centrada em um pino horizontal sem atrito por uma extremidade. A barra é liberada do repouso em uma posição vertical como mostrado na Figura P10.6
Uma demonstração comum, ilustrada na Figura P10.76, consiste em uma bola repousando em uma extremidade de uma mesa uniforme de comprimento l que é presa na outra extremidade e elevada a um ângulo de θ
Suponha que uma pessoa se incline para a frente para levantar um peso “com suas costas”, como mostrado na Figura P10.79a. A coluna vertebral gira principalmente na quinta vértebra lombar com a força d
Uma escada portátil de peso desprezível é construída como mostrado na Figura P10.73, com A C=B C=l=4,00m . Um pintor de massa m=70,0k g sobe na escada d=3,00m do chão. Considerando o piso sem atrito,