Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 13.Problemas Adicionais - Ex. 88
Uma espaçonave está viajando ao longo da reta que liga o centro da Terra ao centro da Lua. A que distância da Terra a força gravitacional total que a Terra e a Lua exercem sobre a a nave é zero?
Passo 1
Para que a força gravitacional total sobre a nave se anule, precisamos ter a seguinte situação:
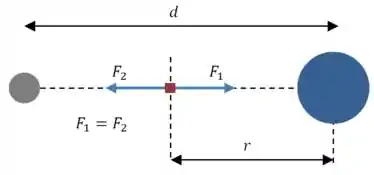
Onde e são as forças gravitacionais exercidas sobre a nave pela Terra e pela Lua, respectivamente.
Perceba que nós só não representamos as forças de reação que a nave exerce sobre a Terra e a Lua porque elas não importam para nós nesse caso.
Passo 2
Agora vamos lembrar das expressões para essas forças:
Agora vamos igualar as duas expressões:
Podemos dividir tudo por e multiplicar cruzado:
Agora vamos isolar os termos ao quadrado e tirar a raiz dos dois lados:
Agora é só substituir os valores e calcular:
Resposta
A força será zero quando a distância até o centro da Terra for .