Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 10.Problemas - Ex. 12
Calcule o período de oscilação de uma partícula no túnel hipotético através do centro da Terra considerado na Seção 10.9 (c). Com que velocidade a partícula passaria pelo centro da Terra? Compare os resultados com os do problema 2.
Passo 1
Cara, o que a gente tem que saber é o seguinte: quando o corpo vai entrando no planeta, tudo que ficou “acima” não exerce mais atração gravitacional. É como se fosse ser atraído só pela parte que ainda é interna, sacou?
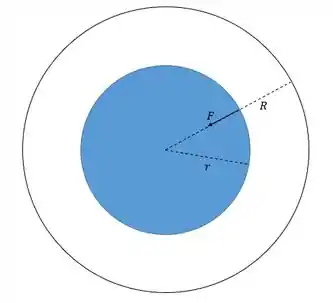
A força de atração gravitacional no corpo é calculada por:
Esse é a massa dessa parte interna de azul! Ela se relaciona com a massa da esfera toda pelo volume, e portanto, pelo raio!
Então a força fica:
Passo 2
Achamos uma expressão bem bonita pra força gravitacional! Tá vendo que ela é dessa forma aqui?
Isso aí é uma força conservativa, ou seja, essa parada é um MHS! E como a gente calcula o período do MHS?
Substituindo:
Substituindo os valores do raio e da massa da Terra...
Passo 3
Pra acharmos a velocidade no centro da Terra, vamos usar conservação de energia! A energia cinética adquirida é igual ao trabalho realizado pela força gravitacional.
Esse trabalho vai se tornar cinética, como já vimos.
Substituindo: